Comment encadrer correctement une suite ?

[psp]

Bonjour,

Je souhaite attirer votre attention sur ce théorème :
Si quelque soit n, Un=
Dans un exercice type nous connaissons Vn mais il sera difficile de calculer sa limite de front. On devra alors formuler deux suites Un et Wn encadrant Vn tout en ayant la même limite.

J'en viens à ma question : Existe t-il une méthode plus ou moins polyvalente permettant de créer ces deux suites Un et Wn ?

Merci beaucoup
Cordialement.

[Alannaria]

La limite L identifiée dépend entièrement de la nature des suites que j'ai : adjacentes en étant définies sur domaine... :dodo:

[Anonyme]

@psp

Ta question est intéressante car na notion de suites adjacentes est très souvent utilisée dans des démonstrations de propriété mathématique
Bien sûr ta question n'est pas assez explicite ( car il y a un tas d'exos sur les suites adjacentes complétement différentes les unes des autres dans le domaine des nombres )


Un exemple, très connu , sur les suites adjacentes est utilisé pour démontrer la propriété suivante :

l'ensemble des nombres rationnels Q est dense dans l'ensemble des nombres réels R


Est ce que tu connais ?

si NON : essaie de travailler la question suivante :
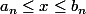
pour tout réel , il faut trouver 2 suites adjacentes et de nombres rationnels qui convergent vers et telles que pour tout n

[Anonyme]

Je souhaite attirer votre attention sur ce théorème :

Bonjour
Notre attention a été attirée et tu as eu quelques réponses à ton message....

Merci de nous donner tes réactions par rapport à nos réponses