Dérivée partielle et dérivée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
albantor30
- Membre Naturel
- Messages: 25
- Enregistré le: 20 Avr 2006, 18:23
-
 par albantor30 » 22 Avr 2006, 12:39
par albantor30 » 22 Avr 2006, 12:39
Bonjour c'est encore moi (je viens de découvrir ce forum et il me plait :lol5:) !
Voila je dois en fait développer ceci :
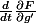
où
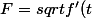^2 sin^2(g(t)) + g'(t)^2})
Ce qui donne :
g' '(t)}{ sqrt{f'(t)^2 sin^2(g(t)) + g'(t)^2} } \right))
Et c'est là que je bloque... Quand je dérive par rapport à

est ce que je dois considérer les fonctions autres que
)
comme des constantes ou dois-je dériver comme ceci :
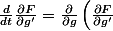 \frac{dg}{dt} + \frac{\partial}{\partial f'} \left( \frac{\partial F}{\partial g'} \right) \frac{df'}{dt} + \frac{\partial}{\partial g'} \left( \frac{\partial F}{\partial g'} \right) \frac{dg'}{dt} + \frac{\partial}{\partial g''} \left( \frac{\partial F}{\partial g'} \right) \frac{dg''}{dt})
?
Merci !
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 22 Avr 2006, 14:17
par abcd22 » 22 Avr 2006, 14:17
Bonjour, je ne comprends pas bien ce que tu dois faire, F est une fonction d'une seule variable t, c'est bizarre de dériver par rapport à g'. Personnellement je dériverais en ne supposant rien constant, en considèrant
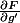
comme une fonction de t ordinaire.
-
zorg
- Membre Naturel
- Messages: 78
- Enregistré le: 21 Avr 2006, 09:17
-
 par zorg » 22 Avr 2006, 15:34
par zorg » 22 Avr 2006, 15:34
Pas calir du tout en effet.
L'expression
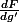
n'a pas de sens.
De toute façon, la fonction F est une fonction d'une seule variable, la variable t. Donc on ne peut dériver F que par rapport à t. Ce qui donne (s'il n'y a pas d'erreur de parenthésage dans l'expression de ton F):
=\frac{n(t)}{d(t)})
avec
=2F(t))
et
=2f'(t)f^{(2)}(t)sin^2(g(t))+(f'(t))^2g'(t)sin(2g(t))+2g'(t)g^{(2)}(t))
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 22 Avr 2006, 16:49
par Pythales » 22 Avr 2006, 16:49
Je vois que tu recherches toujours ta géodésique de sphère !
J'avais calculé l'arc de courbe
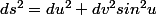
ce qui donne, en utilisant l'équation générale du calcul des variations :
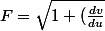^2 sin^2u})
soit en posant
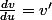
:
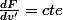
, ce qui doit donner une relation entre u et v.
J'en étais arrivé là, mais la suite est complexe.
-
albantor30
- Membre Naturel
- Messages: 25
- Enregistré le: 20 Avr 2006, 18:23
-
 par albantor30 » 22 Avr 2006, 20:35
par albantor30 » 22 Avr 2006, 20:35
@abcd22 :
Je pense aussi finalement que c'est comme ça... (hélas)
@ zorg:
Là je ne suis pas d'accord avec toi zorg. Dans l'étude du calcul des variations par exemple, on utilise souvent des fonctions à variables liées (je sais pas si on appelle ça comme ça mais bon). Je ne sais pas si tu as entendu parlé de l'équation d'Euler-Lagrange. Elle sert à minimiser une intégrale du type :
, f'(x) \right) dx)
en vérifiant l'équation :
)
De plus, je n'ai jamais parlé de
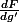
mais bien de
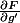
, ce qui change tout.
@Pythales :
En effet, je cherche toujours... J'essayais avec Euler-Lagrange plus ou moins adapté mais je ne savais plus comment dériver. (et puis ça semble aussi un peu compliqué)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités