Devoir maison terminale ES
37 messages
- Page 2 sur 2 - 1, 2
Je ne suis pas sûr du tout non plus...SamanthaN a écrit:J'ai aussi :
On sait que f(-3)=9
donc a(-3)3+ b(-3)2+ c(-3)+ d = 9
-27a - 9b - 3c = 9
f(-3)= c
Donc je peux conclure que c = - 3
mais celui la je ne suis pas sure du tout
Tu sais aussi que la courbe admet une tangente horizontale, cest-à-dire donc le coefficient directeur vaut 0, au point dabscisse 1 et que la droite (OA) est tangente à la courbe au point dabscisse 0.
Comment peux-tu traduire algébriquement le premier point ?
Voilà ce que j'ai trouvé mais je ne sais pas si c'est bon :
La courbe C admet au point B d'abscisse 1 une tangente horizontale c'est à dire que le coefficient directeur de la tangente vaut 0 au point B donc b = 1
La droite (OA) a pour équation y = -3x
La droite (OA) est tangente à la courbe au point d'abscisse 0
(Par lecture graphique nous pouvons voir que) f(-3) est le coefficient directeur de la tangente en -3 donc f(-3) = 1/3
a= 1/3
et pour f(-3) = 9 je ne vois pas comment on fait !!
La courbe C admet au point B d'abscisse 1 une tangente horizontale c'est à dire que le coefficient directeur de la tangente vaut 0 au point B donc b = 1
La droite (OA) a pour équation y = -3x
La droite (OA) est tangente à la courbe au point d'abscisse 0
(Par lecture graphique nous pouvons voir que) f(-3) est le coefficient directeur de la tangente en -3 donc f(-3) = 1/3
a= 1/3
et pour f(-3) = 9 je ne vois pas comment on fait !!
Je suis désolé de te le dire mais tu affirmes nimporte quoi nimporte comment...
La courbe donnée ci-dessous est la représentation graphique dune fonction
donnée ci-dessous est la représentation graphique dune fonction  définie sur
définie sur  dans un repère orthogonal
dans un repère orthogonal ) . La courbe
. La courbe  vérifie les quatre conditions suivantes : elle passe par lorigine
vérifie les quatre conditions suivantes : elle passe par lorigine  du repère et par le point
du repère et par le point ) ; elle admet au point
; elle admet au point 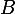 dabscisse
dabscisse  une tangente horizontale et elle admet la droite
une tangente horizontale et elle admet la droite ) pour tangente en
pour tangente en 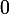 .
.
On suppose que est définie sur
est définie sur  par :
par :
 = ax^3 + bx^2 + cx + d) où
où 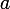 ,
, 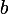 ,
,  et
et 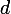 sont des réels.
sont des réels.
Montrer, en utilisant les quatre conditions de départ, que :

1. Traduisons le fait, pour la fonction , que sa courbe représentative
, que sa courbe représentative  passe par lorigine
passe par lorigine  du repère
du repère
=0\hspace{4}\Longleftrightarrow\hspace{3}a\times0^3+b\times0^2+c\times0+d=0\hspace{4}\Longleftrightarrow\hspace{3}d=0) .
.
Conclusion : .
.
2. Traduisons le fait, pour la fonction , que
, que  passe par le point
passe par le point )
=9\hspace{4}\Longleftrightarrow\hspace{3}a\times(-3)^3+b\times(-3)^2+c\times(-3)+d=9\hspace{4}\Longleftrightarrow\hspace{3}-27a+9b-3c=9) .
.
Conclusion : La première équation à résoudre est : .
.
3. Traduisons le fait, pour la fonction , que
, que  admette au point
admette au point 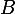 dabscisse
dabscisse  une tangente horizontale
une tangente horizontale
=0) .
.
Or=3ax^2+2bx+c)
Donc=0\hspace{4}\Longleftrightarrow\hspace{3}3a\times1^2+2b\times1+c=0\hspace{4}\Longleftrightarrow\hspace{3}3a+2b+c=0) .
.
Conclusion : La deuxième équation à résoudre est : .
.
4. Traduisons le fait, pour la fonction , que
, que  admette la droite
admette la droite ) pour tangente en
pour tangente en 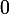
Déterminons dabord léquation de la droite)
Léquation de la droite est une fonction linéaire de la forme (car elle passe par lorigine du repère).
(car elle passe par lorigine du repère).
Le coefficient directeur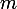 de la droite vaut
de la droite vaut  . Doù
. Doù  .
.
Conclusion :\hspace{1}:\hspace{1}y_{(OA)}=-3x)
Déterminons ensuite léquation de la tangente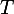 à
à  au point dabscisse
au point dabscisse 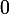
(x-0)+f(0)=\left(3a\times0^2+2b\times0+c\right)x=cx)
Conclusion :
Or,) est tangente à
est tangente à  en
en 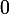 , donc on a
, donc on a }=y) .
.
}=y\hspace{4}\Longleftrightarrow\hspace{3}-3x=cx\hspace{4}\Longleftrightarrow\hspace{3}c=-3)
Conclusion : .
.
À toi de terminer...
La courbe
On suppose que
Montrer, en utilisant les quatre conditions de départ, que :
1. Traduisons le fait, pour la fonction
Conclusion :
2. Traduisons le fait, pour la fonction
Conclusion : La première équation à résoudre est :
3. Traduisons le fait, pour la fonction
Or
Donc
Conclusion : La deuxième équation à résoudre est :
4. Traduisons le fait, pour la fonction
Déterminons dabord léquation de la droite
Léquation de la droite est une fonction linéaire de la forme
Le coefficient directeur
Conclusion :
Déterminons ensuite léquation de la tangente
Conclusion :
Or,
Conclusion :
À toi de terminer...
Bonjour,SamanthaN a écrit:Merci beaucoup mais pour terminer je dois bien trouver une autre équation afin que ça fasse un système, je le résouds et j'ai les solutions ensuite non?
Non, tu les as toutes.
Noublie pas que tu sais que
37 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 105 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
