Bonjour,
Je dois faire un DM mais j'ai vraiment du mal avec les intégrales ...
Voici le sujet :
On a une fonction f définie sur ]0 ; +infini[ tel que f(x) = 2lnx / x²+x. Supposition : 1« x « 3/2
1. Je dois étudier le signe de h(x) sachant que h(x) = f(x) - lnx/x² .
Puis je dois montrer que lnx/x² « f(x).
2. Ensuite je dois montrer que f(x) « lnx/x.
3. a) Je dois calculer la valeur exacte de I = intégrale (de 3/2 à 1) de (lnx/x) dx.
b) Avec l'intégration par parties, je dois calculer la valeur extacte de J = intégrale (toujours de 3/2 à 1) (lnx/x²) dx.
4. Grâce aux questions précedentes, je dois trouver un encadrement de K = intégrale (toujours de 3/2 à 1) f(x) dx.
Pour le signe de h(x), un tableau de signe suffit ? Je sais que h(x) s'annule quand x=1 et que le signe de h(x) est toujours positif. Mais je m'arrive pas à montrer ce que l'on me demande :s Quelqu'un pourrait m'aider ? Merci d'avance :happy2:
Devoir Maison (Intégrales) Terminale S
15 messages
- Page 1 sur 1
par Ben314 » 21 Fév 2010, 11:29
Salut,
Ta fonction est=2\frac{\ln(x)}{x^2}+x)
ou bien =2\frac{\ln(x)}{x^2+x})
?
Vu ce que tu as écrit, je pense qu'il s'agit de la première.
On a donc=f(x)-\frac{\ln(x)}{x^2}=\frac{\ln(x)}{x^2}+x)
et on en déduit que >0)
si et seulement si +x^3>0)
(car 
).
Pour déterminer où est ce que=\ln(x)+x^3)
est positif, je te conseillerais d'étudier les variations de cette fonction (i.e. de calculer la dérivée)...
Ta fonction est
Vu ce que tu as écrit, je pense qu'il s'agit de la première.
On a donc
Pour déterminer où est ce que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par melidu42 » 21 Fév 2010, 11:46
Je suis désolée, c'est la première fois que j'utilise ce site je ne sais pas vraiment comment écrire sous forme de fraction.
Ma fonction est : f(x) = (2lnx)/(x²+x), je suis désolée c'est moi qui ait oublié les parenthèses :S
Ma fonction est : f(x) = (2lnx)/(x²+x), je suis désolée c'est moi qui ait oublié les parenthèses :S
par Ben314 » 21 Fév 2010, 12:12
Bon, reprenons...
(si tu compte passer de temps en temps sur le site, tu peut regarder comment on fait "de belles formules" en latex : c'est pratique)
 =2\frac{\ln(x)}{x^2+x}=2\frac{\ln(x)}{x(x+1)})
donc
=f(x)-\frac{\ln(x)}{x^2}=\ln(x)\frac{2x-(x+1)}{x^2(x+1)}=\ln(x)\frac{x-1}{x^2(x+1)})
.
Tu peut étudier le signe à l'aide d'un tableau, mais ce n'est pas vraiment utile : sur l'intervalle considéré, tout les facteurs de h(x) sont positifs donc h est positif.
Aprés, c'est complètement con, vu que=f(x)-\frac{\ln(x)}{x^2}\geq 0)
sur l'intervalle, cela signifie que \geq\frac{\ln(x)}{x^2})
sur l'intervalle.
Pour la deux, tu procède exactement de la même façon que pour la 1) en cherchant le signe de=f(x)-\frac{\ln(x)}{x})
.
Pour la trois a), il faut trouver une primitive de}{x})
. Si on ne l'a jamais vu, ce n'est pas super façile.
Une indic. : Si on pose=\ln(x))
, que vaut )
?
Comment peut on écrire à l'aide de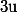 
et 
? Conclusion...
Pour la trois b), as-tu vu les intégrations "par parties" ?
Le 4) est évident...
(si tu compte passer de temps en temps sur le site, tu peut regarder comment on fait "de belles formules" en latex : c'est pratique)
Tu peut étudier le signe à l'aide d'un tableau, mais ce n'est pas vraiment utile : sur l'intervalle considéré, tout les facteurs de h(x) sont positifs donc h est positif.
Aprés, c'est complètement con, vu que
Pour la deux, tu procède exactement de la même façon que pour la 1) en cherchant le signe de
Pour la trois a), il faut trouver une primitive de
Une indic. : Si on pose
Comment peut on écrire
Pour la trois b), as-tu vu les intégrations "par parties" ?
Le 4) est évident...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par melidu42 » 21 Fév 2010, 12:18
Merci beaucoup.
La primitive de (lnx)/x est (lnx)²/2 :) Mais je ne comprend pas comment calculer l'intégrale à partir de la primitive.
L'intégration par parties, nous l'avons vu un peu en cours mais c'est quelque chose que j'ai encore du mal à comprendre =/
La primitive de (lnx)/x est (lnx)²/2 :) Mais je ne comprend pas comment calculer l'intégrale à partir de la primitive.
L'intégration par parties, nous l'avons vu un peu en cours mais c'est quelque chose que j'ai encore du mal à comprendre =/
par Ericovitchi » 21 Fév 2010, 12:41
quand tu as une fonction f(x) et que tu connais déjà une primitive F(x)
alorsdx = [F(x)]^b_a=F(b)-F(a))
Sinon l'intégration par partie ça consiste à dire :
v'(x) dx = [u(x)v(x))]^b_a - \bigint_{a}^{b} v(x)u'(x) dx)
alors
Sinon l'intégration par partie ça consiste à dire :
par melidu42 » 21 Fév 2010, 12:54
Si j'ai bien compris, la valeur exacte de I est (lnx)² / 4 ? :)
Pour l'intégration par parties, j'ai un peu plus de mal car je me demande si c'est (lnx)/(x²) qui représente u(x) dans la formule que vous m'avez donné.
En tout cas, merci beaucoup pour votre aide :)
Pour l'intégration par parties, j'ai un peu plus de mal car je me demande si c'est (lnx)/(x²) qui représente u(x) dans la formule que vous m'avez donné.
En tout cas, merci beaucoup pour votre aide :)
par Ben314 » 21 Fév 2010, 13:18
non, vu que "I = intégrale (de 3/2 à 1) de (lnx/x) dx", la quantité I ne dépend de.. rien : c'est l'aire sous la courbe entre deux droites fixées.melidu42 a écrit:Si j'ai bien compris, la valeur exacte de I est (lnx)² / 4 ?
Reprend la formule qu'Ericovitchi t'as donné et n'oublie pas de remplacer a et b par les valeurs dont te parle l'exercice !!!
Dans la formule qu'Ericovitchi te donne on peut prendre absolument tout ce que l'on veut pour u(x) et v(x), MAIS, le but est évidement de rendre le calcul plus simple et surtout pas de le rendre plus compliqué !!!melidu42 a écrit:Pour l'intégration par parties, j'ai un peu plus de mal car je me demande si c'est (lnx)/(x²) qui représente u(x) dans la formule que vous m'avez donné.
Par exemple, si on applique la formule ici, cela signifie que l'on veut que
Voila des exemples de ce que l'on pourait prendre :
a)
b)
c)
d)
etc...
Il faut trouver le "choix astucieux" qui va simplifier la formule : aprés utilisation de la formule, on aura du
A ton avis, quel est le bon choix (les premières fois que l'on utilise cette formule, on est forcément un peu "paumé"..) ?
P.S. Pour t'aider un peu, le "bon choix" fait partis des 4 que je t'ais donné...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par melidu42 » 21 Fév 2010, 13:26
Pour la question 3. a) quand je calcule I, j'arrive à :
I = [((lnx)²)/2 * (3/2)] - [((lnx)²/2) * 1]
I = [3(lnx)² - (lnx)²] / 4
I = (lnx)² / 4
Non ? :s
Je suis vraiment perdue pour l'intégration par parties, peut-être que je choisirais le petit c) .. :S Est-ce bon ?
P.S : Quelqu'un pourrait m'expliquer comment mettre mes calculs sous forme de fraction, ça simpliferait la lecture pour vous :S svp.
I = [((lnx)²)/2 * (3/2)] - [((lnx)²/2) * 1]
I = [3(lnx)² - (lnx)²] / 4
I = (lnx)² / 4
Non ? :s
Je suis vraiment perdue pour l'intégration par parties, peut-être que je choisirais le petit c) .. :S Est-ce bon ?
P.S : Quelqu'un pourrait m'expliquer comment mettre mes calculs sous forme de fraction, ça simpliferait la lecture pour vous :S svp.
par Ben314 » 21 Fév 2010, 13:36
Quand on calcule par exemple F(3/2), attention à bien remplacer tout les x par 3/2 (et pas la moitié...)melidu42 a écrit:Pour la question 3. a) quand je calcule I, j'arrive à :
I = [((ln 3/2 )²)/2 * (3/2)] - [((ln 1 )²/2) * 1]
Bien joué : effectivement, dans le c) le u' et le v sont trés simple cela permet de "simplifier" l'expression.melidu42 a écrit:Je suis vraiment perdue pour l'intégration par parties, peut-être que je choisirais le petit c) .. :S Est-ce bon ?
Ne t'inquiète pas, à force d'en faire, on finit par voir assez bien qui il faut prendre pour u et v' mais au début, c'est pas super façile...
1ère solution : tu ouvre le post "Important : Ecrire des belles formules mathématiques - balises TEX" de uztop (deuxième dans le forum lycée) qui explique trés bien.P.S : Quelqu'un pourrait m'expliquer comment mettre mes calculs sous forme de fraction, ça simpliferait la lecture pour vous :S svp.
2em solution : tu clique sur la case "citer" d'un post où tu trouve que la présentation est "trés jolie" et tu regarde comment le type à fait pour obtenir ce résultat, puis tu fait un copier-coller.
Le mieux, c'est... les deux méthodes.
P.S. Par exemple, j'ai pompé sur dinozzo ( :zen: s'il est là) pour voir comment il faisait des formules "ENOOOOORMES" : je sais pas où il a trouvé le fait que l'on peut mettre des 3$ ou des 4$ au début (maintenant que j'ai pompé, je m'en fout, mais j'aimerais bien avoir la réponse quand même).
P.S.2 : Je "pompe" aussi beaucoup de formules sur le site mimeTeX user's manuel que j'ai mis dans mes "favoris" (si on clique sur une jolie formule, il donne le codage...)
Exemple :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par melidu42 » 21 Fév 2010, 13:53
Il faudrait que je prenne le temps de regarder tout ça, merci beaucoup pour les conseils :)
Pour I je trouve : I = 3(ln3/2)² / 4. C'est bon cette fois ? :S
Pour I je trouve : I = 3(ln3/2)² / 4. C'est bon cette fois ? :S
par Ben314 » 21 Fév 2010, 14:23
Perso je (ou plutôt maple) trouve I = (ln3/2)² / 2.... (erreur de calcul ?)
a condition que l'intégrale soit de 1 à 3/2 (et pas de 3/2 à 1)
a condition que l'intégrale soit de 1 à 3/2 (et pas de 3/2 à 1)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par melidu42 » 21 Fév 2010, 15:00
Mais l'intégrale va de 3/2 à 1 je crois :s
Enfaite le 3/2 est situé en haut et le 1 est situé en bas :S
Un petit schèma improvisé :
3/2
|
|
1
J'espère que vous comprendrez. Si c'est ainisi, est-ce que ma réponse est juste ? :)
Enfaite le 3/2 est situé en haut et le 1 est situé en bas :S
Un petit schèma improvisé :
3/2
|
|
1
J'espère que vous comprendrez. Si c'est ainisi, est-ce que ma réponse est juste ? :)
par Ben314 » 21 Fév 2010, 15:18
Si le 1 est en bas et le 3/2 en haut, cela se prononce à l'oral "intégrale de 1 à 3/2".
La plupart du temps, quand on "intégre de a à b", c'est avec a<b (il y a des exeptions mais en term., je sais pas si on en parle...)
Donc tu as juste une petite erreur de simplification...
-F(1)\)
où =\frac{(\ln(x))^2}{2}\)
 \right)^2 -\frac{1}{2}\left(\ln\left(1\right)\right)^2)=\frac{1}{2}\left(\ln\left(\frac{3}{2} \right) \right)^2=\frac{1}{2}\left(\ln(3)-\ln(2)\right)^2)
vu que =0)
P.S. : J'avais mal corrigé ton erreur dans le début du post 10...
La plupart du temps, quand on "intégre de a à b", c'est avec a<b (il y a des exeptions mais en term., je sais pas si on en parle...)
Donc tu as juste une petite erreur de simplification...
P.S. : J'avais mal corrigé ton erreur dans le début du post 10...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par melidu42 » 21 Fév 2010, 15:26
Ah je comprend petit à petit, merci beaucoup :)
Pour la question 3) b. je trouve : J = [- (2/3) ln(3/2)] + 1/3
Est-ce juste ? :)
Pour la question 3) b. je trouve : J = [- (2/3) ln(3/2)] + 1/3
Est-ce juste ? :)
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :