Devoir maison terminale ES

[SamanthaN]

Bonjour,

La courbe (C) donnée ci dessous est la représentative graphique d'une fonction f définie sur [-3 ; 3] dans un repère orthogonal (O, i , j). La courbe C vérifie les quatre conditions suivantes : elle passe par l'origine O du repère et par le point A (-3 ; 9); elle admet au point B d'abscisse 1 une tangente horizontale et elle admet la droite (OA) pour tangente en 0

On suppose que f est définie sur [ -3 ; 3 ] par:
f(x) = ax3 + bx2 + cx + d où a, b, c ,d sont des réels.
Montrer que en utilisant les quatre conditions de départ que:
a = 1/3
b = 1
c = -3
d = 0

Je suis bloquée a cette question, pouvez vous m'aider svp
Merci d'avance

[Alp]

La courbe passe par l’origine du repère, le point appartient donc à la courbe, donc . Remplace par la définition de la fonction avec 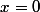et vois ce que tu peux en conclure pour .

Tu sais aussi que . Comment peux-tu traduire en terme de dérivée le fait que la courbe admet au point B d’abscisse une tangente horizontale ?

Enfin, donne l’équation de la droite et traduis mathématiquement le fait qu’elle est tangente à la courbe en .

[SamanthaN]

Ce que vous m'avez dit ne m'a pas beaucoup aidé, j'ai réussi quelques petites choses mais pas tout !! Mais merci quand même.

[Jimm15]

Ce que vous m'avez dit ne m'a pas beaucoup aidé, j'ai réussi quelques petites choses mais pas tout !! Mais merci quand même.

Bonjour,

N’hésite pas à dire où tu bloques.
On t’aidera sans problème.

[SamanthaN]

Eh bien, je ne comprends tout simplement pas certaines explications qu'il m'a donné donc je n'arrive pas à avancer.

[Jimm15]

La courbe passe par l’origine du repère, le point appartient donc à la courbe, donc .
==> Jusque là, je suppose que c’est OK.

Remplace par la définition de la fonction avec et vois ce que tu peux en conclure pour .
==> Prends l’expression de la fonction et remplace par . Tu sais que le résultat vaut (puisque ). Conclusion ?

Tu sais aussi que .
==> Là aussi, je pense qu’il n’y a pas de problème.

Comment peux-tu traduire en terme de dérivée le fait que la courbe admet au point B d’abscisse une tangente horizontale ?
==> On se ramène à la définition du nombre dérivé d’une fonction en . Elle a un rapport direct avec la tangente à la courbe en .

Enfin, donne l’équation de la droite et traduis mathématiquement le fait qu’elle est tangente à la courbe en .
==> Détermine d’abord l’équation de la droite. Ensuite, quelle est l’équation générale de la tangente à une fonction en ?

À toi. :id:

[SamanthaN]

Merci beaucoup, c'est surtout les derniers points que je comprenais pas trop comment faire, comment justifier ... Je vais réessayer maintenant et je verrais bien! Encore merci ;)

[SamanthaN]

J'ai fait ça :
La courbe passe par l'origine du repère, le point O (0;0), appartient donc à la courbe, donc f(O) = 0

f(x) = ax3 + bx2 + cx + d
f(0) = a(0)3 + b (0)2 + c(0) + d
= 0
Je peux donc conclure que d = 0

On sait que f (-3) = 9

Le nombre dérivé d'une fonction en a est le coefficient directeur de la tangente de la courbe (C) de f en a
f'(a) est la coefficient directeur de la tangente en a donc f'(a) = 1/3

Voilà je ne sais pas si c'est bon, pouvez vous me dire svp ?
et je n'arrive pas a justifier avec le point B d'abscisse 1 une tangente horizontale

[SamanthaN]

J'ai oublié aussi : l'équation de la droite (OA) est y= -3x

[Jimm15]

J'ai fait ça :
La courbe passe par l'origine du repère, le point O (0;0), appartient donc à la courbe, donc f(O) = 0

f(x) = ax3 + bx2 + cx + d
f(0) = a(0)3 + b (0)2 + c(0) + d
= 0
Je peux donc conclure que d = 0

On sait que f (-3) = 9

==> Jusque là, c’est OK.

Le nombre dérivé d'une fonction en a est le coefficient directeur de la tangente de la courbe (C) de f en a
f'(a) est la coefficient directeur de la tangente en a donc f'(a) = 1/3

Voilà je ne sais pas si c'est bon, pouvez vous me dire svp ?
et je n'arrive pas a justifier avec le point B d'abscisse 1 une tangente horizontale

À la fin, ça ne convient pas.

Attention ! ne correspond pas ici au coefficient de l’équation de la courbe de [/TEX].
C’est une abscisse et uniquement ça.

Quel est le coefficient directeur d’une droite horizontale ? Quel est alors le coefficient directeur de la tangente à la courbe au point d’abscisse ? Quelle est donc la valeur du nombre dérivé ?

Pour la dernière condition, commence par trouver l’équation de la droite .

[Jimm15]

J'ai oublié aussi : l'équation de la droite (OA) est y= -3x

Très bien.
Quelle est l’équation générale de la tangente à la courbe de au point d’abscisse ?

[SamanthaN]

Je me perds là, je ne comprends plus rien !
Le coefficient directeur d'une tangente horizontale est 0, non ? Donc le coefficient directeur de la tangente à la courbe au point B d'abscisse a = 1
La valeur du nombre dérivée de f'(1) = 0 mais je ne suis pas sure du tout.
Et l'équation de la droite (OA) est y = -3x

[Jimm15]

Je me perds là, je ne comprends plus rien !
Le coefficient directeur d'une tangente horizontale est 0, non ? Donc le coefficient directeur de la tangente à la courbe au point B d'abscisse a = 1
La valeur du nombre dérivée de f'(1) = 0 mais je ne suis pas sure du tout.
Et l'équation de la droite (OA) est y = -3x

C’est exact.

Maintenant, regarde mon message précédent et essaie de répondre à ma question.

[SamanthaN]

Cette question : Quelle est l’équation générale de la tangente à la courbe de \large f au point d’abscisse \large a ? Je ne comprends pas car l'équation de la tangente est y = -3x mais il n'y a rien d'autre à chercher la, je l'ai déjà l'équation

[Jimm15]

Cette question : Quelle est l’équation générale de la tangente à la courbe de \large f au point d’abscisse \large a ? Je ne comprends pas car l'équation de la tangente est y = -3x mais il n'y a rien d'autre à chercher la, je l'ai déjà l'équation

Je suis d’accord mais avoir cette équation n’aide en rien à déterminer les coefficients de ta fonction polynôme.
C’est pour cela qu’on va essayer de traduire le fait que cette droite soit tangente à la courbe de au point d’abscisse . Et pour cela, il n’y a qu’un moyen : revenir à la définition de l’équation d’une tangente à la courbe d’une fonction au point d’abscisse . Comme cette équation fait intervenir et , cela nous permettra de déterminer certains coefficients de l’expression de .

Dis-moi si tu ne comprends pas.

[SamanthaN]

Je commence à comprendre mais je ne vois pas comment on fait pour trouver ça =S

[Jimm15]

Je reprends le cours :

Équation de tangente

est une fonction définie sur un intervalle et dérivable en , , sa courbe représentative dans un repère. La tangente en (ou au point d’abscisse ) à a pour équation :
[CENTER][/CENTER]

[SamanthaN]

Ah oui, je vois maintenant ! mais comment on ne connait pas la fonction ... comment fait on ?

[Jimm15]

Ah oui, je vois maintenant ! mais comment on ne connait pas la fonction ... comment fait on ?

On utilise uniquement ce qu’on sait sur elle, et ça suffit.
sera fonction des coefficients de encore indéterminés.

[SamanthaN]

d'accord, je te remercie pour toute ton aide