Aide DM 1ere S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 26 Oct 2010, 21:32
par Jimm15 » 26 Oct 2010, 21:32
Il ne faut plus quil y ait de
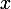
dans léquation sinon on ne peut pas la résoudre.
Je vais transformer un peu lécriture de léquation :
)
.
À toi de mécrire ça en fonction de
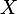
uniquement.
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 26 Oct 2010, 22:10
par zepl0w » 26 Oct 2010, 22:10
X² - 4X +2 est donc faux ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 26 Oct 2010, 22:20
par Jimm15 » 26 Oct 2010, 22:20
zepl0w a écrit:X² - 4X +2 est donc faux ?
Cest juste sauf pour le

qui fait partie de

...
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 27 Oct 2010, 08:20
par zepl0w » 27 Oct 2010, 08:20
Bonjour,
5.On pose X = x + 1/x
(E) = x² - 4x + 2 - 4/x + 1/x² = 0 équivaut à x² + 1/x² - 4x - 4/x + 2
donc x² + 1/x² = a ; - 4x - 4/x = b et 2 = c.
Je ne comprend donc pas pourquoi le +2 est faux.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 27 Oct 2010, 08:46
par Jimm15 » 27 Oct 2010, 08:46
zepl0w a écrit:Bonjour,
5.On pose X = x + 1/x
(E) = x² - 4x + 2 - 4/x + 1/x² = 0 équivaut à x² + 1/x² - 4x - 4/x + 2
donc x² + 1/x² = a ; - 4x - 4/x = b et 2 = c.
Je ne comprend donc pas pourquoi le +2 est faux.
Bonjour,
Je ne comprends pas ce que tu écris.

et

.
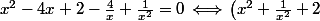 - 4x - \frac{4}{x} = 0 \hspace{2} \Longleftrightarrow \hspace{1} \left(x^2 + \frac{1}{x^2} + 2\right) - 4\left(x + \frac{1}{x}\right) = 0 \hspace{2} \Longleftrightarrow \hspace{1} X^2-4X=0)
.
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 27 Oct 2010, 09:10
par zepl0w » 27 Oct 2010, 09:10
Je viens de comprendre merci pour cette explication. :we:
Ensuite on calcule ;) avec a = 1 ; b = -4 et c = 0.
;) = 16
X' = 4 - 4 /2
X' = 0
X'' = 4 +4 /2
X'' = 4
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 27 Oct 2010, 09:25
par Jimm15 » 27 Oct 2010, 09:25
Ce nest pas nécessaire ici :
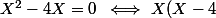=0 \hspace{5} \Longleftrightarrow \hspace{4} X=0 \hspace{4} \text{ou} \hspace{4} X=4)
.
Quand 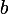 ou
ou  est nul dans un trinôme du second degré, pense quil nest pas nécessaire de calculer le discriminant pour en trouver les racines ; cest superflu puisquon peut les trouver plus facilement avec moins de calculs.
est nul dans un trinôme du second degré, pense quil nest pas nécessaire de calculer le discriminant pour en trouver les racines ; cest superflu puisquon peut les trouver plus facilement avec moins de calculs.
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 27 Oct 2010, 10:25
par zepl0w » 27 Oct 2010, 10:25
0 et 4 sont les solutions de (E')
donc x = 0 + 1/0
x = 0
ou x = 4 + 1 /4
x = 17/4
L'équation (E) a pour solution 0 et 17/4 ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 27 Oct 2010, 10:36
par Jimm15 » 27 Oct 2010, 10:36
zepl0w a écrit:0 et 4 sont les solutions de (E')
donc x = 0 + 1/0 Oh !
x = 0
ou x = 4 + 1 /4
x = 17/4
L'équation (E) a pour solution 0 et 17/4 ?
Je ne comprends pas ta méthode de résolution.
On a

et

.
Or

.
Doù

ou

.
Je te laisse résoudre.
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 27 Oct 2010, 12:19
par zepl0w » 27 Oct 2010, 12:19
Oui autant pour moi. J'ai bêtement remplacé x par les solution de (E').
x + 1/x = 0 équivaut à x² -1 =0 équivaut à x =1 ou x = -1
x+ 1/x = 4 équivaut à -x² +4x -1 = 0 avec a = -1 ; b = 4 ; c = -1
;) = 12
D'ou x' = 2 + ;)3
et x'' = 2 - ;)3
L'équation (E) a pour solution : -1 ; 2 - ;)3 ; 1 ; 2 + ;)3 ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 27 Oct 2010, 12:29
par Jimm15 » 27 Oct 2010, 12:29
zepl0w a écrit:Oui autant pour moi. J'ai bêtement remplacé x par les solution de (E').
x + 1/x = 0 équivaut à x² -1 =0 équivaut à x =1 ou x = -1x+ 1/x = 4 équivaut à -x² +4x -1 = 0 avec a = -1 ; b = 4 ; c = -1

= 12
D'ou x' = 2 +

3
et x'' = 2 -

3
L'équation (E) a pour solution : -1 ; 2 -

3 ; 1 ; 2 +

3 ?
Attention ! Tu as changé un signe en un autre !!
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 27 Oct 2010, 12:35
par zepl0w » 27 Oct 2010, 12:35
Ah oui.
Donc x + 1 / x = 0 équivaut à x² = - 1 équivaut à x² + 1 = 0 (donc on ne peut pas utiliser l'identité remarquable) équivaut à x + 1 = 0 équivaut à x = -1
(E) n'a donc que 3 solutions ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 27 Oct 2010, 12:50
par Jimm15 » 27 Oct 2010, 12:50
zepl0w a écrit:Ah oui.
Donc x + 1 / x = 0 équivaut à x² = - 1 équivaut à x² + 1 = 0 (donc on ne peut pas utiliser l'identité remarquable) équivaut à x + 1 = 0 équivaut à x = -1
(E) n'a donc que 3 solutions ?

, cest résoluble ça, dans
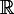
?
-
zepl0w
- Membre Naturel
- Messages: 34
- Enregistré le: 26 Oct 2010, 12:22
-
 par zepl0w » 27 Oct 2010, 13:17
par zepl0w » 27 Oct 2010, 13:17
Je suis bête.
Un carré est toujours positif donc (E) n'a que 2 solutions.
Merci.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
= 12
3
3
3 ; 1 ; 2 +
3 ?