Complexe et barycentre -exercice

[loytef]

Bonjour,

J'ai a résoudre cette exercice :

1) Pour tout nombre complexe z, on considère : f (z) = z^4;)10z^3 + 38z²;)90z+261.

a. Soit b un nombre réel. Exprimer en fonction de b les parties réelle et imaginaire de f(ib).
En déduire que l’équation f (z) = 0 admet deux nombres imaginaires purs comme solution.
>>ok -3i et 3i
b. Montrer qu’il existe deux nombres réels ;) et ;), que l’on déterminera, tels que, pour tout
nombre complexe z, f (z) = (z² + 9)(z² + ;)z + ;)).
>>;)=-10 ; ;)=29
c. Résoudre dans l’ensemble des nombres complexes l’équation f (z) = 0.
>> solutions: 3i;-3i;5+2i;5-2i

2) Le plan complexe P est rapporté à un repère orthonormal.

a. Placer dans le plan P les points A, B, C et D ayant respectivement pour affixes :
Za = 3i, Zb = ;)3i, Zc = 5 + 2i ET Zd = 5 ;) 2i.

b. Déterminer l’affixe de l’isobarycentre G des points A, B, C, D.

c. Déterminer l’ensemble E des points M de P tels que :
|| vecMA + vecMB + vecMC + vecMD || =10.

d.Tracer E sur la figure précédente.

J'ai réussi toute la partie 1 mais je n'arrive pas à faire la partie 2 sur les barycentres.
Quelqu'un peut-il m'aider ?
merci

[Dinozzo13]

Salut !

II : 1°) Quand on te dis qu'un point A a pour affixe , c'est comme si on te disait de placer le point A de coordonnées (x;y)
2°) Cela revient à déterminer les coordonnées de G
3°) G est l'isobarycentre des points A, B, C et D donc d'après la propriété fondamentale, pour tout point M du plan :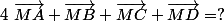
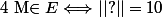, c'est-à-dire, ?=10 ...

[loytef]

D'accord pour le 2)1
Mais comment déterminer les coordonnées de G?

[Dinozzo13]

C'est le cours de 1re S :hum:

Si G est le barycentre de (A,a),(B,b),(C,c) avec A(x,y), B(x',y') et C(x'',y'') alors :
et

[loytef]

oui effectivement j'ai oublié cette formule :triste:

Donc si j'ai bien compris :

Xg = (0+0+5+5)/4 et Yg=(3-3+2-2)/4

Donc coordonnée de G= 2.5
c'est correct?
merci

[loytef]

Si quelqu'un peut m'aider pour la question 2c :triste:
Déterminer l’ensemble E des points M de P tels que :
|| vecMA + vecMB + vecMC + vecMD || =10.

merci

[annick]

Bonjour,
dans ce genre d'exercice, la méthode est toujours sensiblement la même :
tu as G l’isobarycentre des points A, B, C, D. Donc la relation vectorielle qui va avec : GA+.........=0 (tout ça en vecteurs).
Tu cherches à arranger vecMA + vecMB + vecMC + vecMD et pour cela tu utilises Chasles en introduisant G.
Et après tu dois voir que ça te permettra de répondre à ta question.

[loytef]

Désolé mais je ne comprend toujours pas.
vecGA+vecGB+vecGC+vecGD=vec0 & vecMA + vecMB + vecMC + vecMD

Où est-ce qu'on introduit G?
Je vois aucune posibilité d'utiliser Chasle dedans.

merci

[loytef]

Peut être :

||(MG+GA)+(MG+GB)+(MG+GC)+(MG+GD) ||=10 (en vecteur)
mais après?

[Dinozzo13]

Déterminer l’ensemble E des points M de P tels que :
|| vecMA + vecMB + vecMC + vecMD || =10.

Nommes soit G l'isobraycentre de A, B, C et D.
D'après la propriété fondamentale, pour tout point M du plan :

Ensuite,

[loytef]

<==> ||vec4MG||=10 ?? sinon je vois pas.
merci

[Dinozzo13]

oui c'est ça :+++:

[loytef]

Ok mais comment tracer E dans le plan à partir de ||vec4MG||=10 ? ||vecMG||=2.5 ?
merci

[annick]

Si llMGll=cte cela veut dire que M tourne autour de G, toujours à la même distance et donc qu'il se déplace sur le cercle de centre G et de rayon R=cte

[Jimm15]

Bonsoir,

Pour tous points et du plan et pour tout réel , on a l’égalité suivante : .

[loytef]

Merci pour vos réponses.

Donc si j'ai bien compris je dois tracer un cercle de rayon R=40 et de centre G. Mais R=40 dans un repère orthonormé c'est énorme non?

[Jimm15]

Bonjour,

40 ??? :doh:

.

[loytef]

Oui effectivement j'ai mal appliqué l'égalité. :dingue:

Merci à vous :we: