[DM-Nombre Complexe-Barycentre-Bissectrice]

par **Mushroom** » 11 Jan 2009, 12:23

Bonjour,

[font=Verdana]J'ai quelques soucis à comprendre l'énoncé. De plus je crois qu'il y a une erreur...[/font]

Voici l'enoncé :

Voilà je pense qu'il y a 2 erreurs :

il manque un "i" dans la troisième question dans pour le exponentiel en facteur

et ax-by = 0 serait ax+by = 0 (mais là je suis pas sûr)

Mon problème ?
Si comme je pense il manque un "i" dans la question 3, les questions auxquelles je n'arrive pas à répondre sont 3a-b et 4

Voilà je ne demande pas des réponses completes, juste que vous me mettez sur la piste

Merci

par **XENSECP** » 11 Jan 2009, 12:34

Oui il manque un i ^^

Et c'est bien ax - by = 0 ;)

par **Mushroom** » 11 Jan 2009, 12:40

ah c'est bien ce que je pensais ^^

donc pour avoir

ax-by = 0 ?

pouvez vous m'aidez :happy2:

par **XENSECP** » 11 Jan 2009, 12:43

Développe simplement les

par **Mushroom** » 11 Jan 2009, 12:48

j'obtiens
axe^i(alpha-beta/2) + bye^i(beta-alpha/2) = un réel

normalement arg du nombre est égal a 0(2pi)

apres je suis bloqué

par **XENSECP** » 11 Jan 2009, 12:51

lol j'étais déjà à l'étape suivante !
Allez on met les neurones en action "Champignon" :D

par **Mushroom** » 11 Jan 2009, 13:08

franchement je ne voit pas ^^"

déjà la seul maniere d'obtenir le résulat c'est que le réel soit nul

et qu'on est alpha-beta/2 = 0 et beta-alpha/2 = pi

par **XENSECP** » 11 Jan 2009, 13:17

Oula ! OMG !!! Non le réel est pas forcément nul ! Parce que tu veux un résultat sur ax et by pas sur alpha et bêta !

Développe les exponentielles !!

par **Mushroom** » 11 Jan 2009, 13:18

ahhhh non je vois ou tu veux en venir ><

par **Mushroom** » 11 Jan 2009, 13:26

axe^i(alpha-beta/2) + bye^i(beta-alpha/2) = un réel

tu veux dire encore développer ces expo ?
axe^i(alpha/2)e^(-ibeta/2) + bye^i(beta/2)e^(-ialpha/2) = un réel

désolé je trouve pas ça evident ^^"

par **Mushroom** » 11 Jan 2009, 14:02

axe^i(alpha-beta/2) + bye^i(beta-alpha/2) = un réel

tu veux dire encore développer ces expo ?
axe^i(alpha/2)e^(-ibeta/2) + bye^i(beta/2)e^(-ialpha/2) = un réel

désolé je trouve pas ça evident ^^"

pourtant je suis sûr que la réponse me au nez avec le "en déduire.." -_-

c'est raggeant ce genre de question

par **XENSECP** » 11 Jan 2009, 14:08

RRRRRR

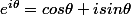
Me dis pas que tu n'as jamais vu cette formule !!!

par **Mushroom** » 11 Jan 2009, 15:28

bon j'ai avancé mais ... enfin tu verras :p

en développant les expo j'ai :

ax[cos(alpha-beta)/2 + i sin(alpha-beta/2)] + by [cos (beta-alpha)/2 + i sin (beta-alpha)/2]

apres transformations, j'ai fait partie réel et partie Imaginaire ça donne ça

(cos(alpha-beta/2))*(ax+by) + i((sin(alpha-beta)/2)(-ax-by))= réel

ssi la partie imaginaire = 0

donc (sin(alpha-beta)/2)(ax-by) = 0
ssi ax=by et sin (bidule chouette) = sin 0
on aboutit a alpha = beta

donc il nous reste

(cos(alpha-beta/2))*(ax+by)
= cos 0*ax+by = ax+by = 2ax -_-

j'ai du me tromper dans un signe qq part mais je vois pas ou

par **XENSECP** » 11 Jan 2009, 15:31

On n'aboutit pas à alpha et bêta au contraire ;)
On aboutit à ax = by ;) Et aucune indication sur alpha et bêta vu qu'on connait pas le réel ;)

par **Mushroom** » 11 Jan 2009, 15:36

ben on a ça

donc (sin(alpha-beta)/2)(ax-by) = 0
ssi ax-by=0 ou sin (bidule chouette) = sin 0

ahhh mais tu veux dire qu'a partir de l'a on peut s'arreter :id:

par **XENSECP** » 11 Jan 2009, 15:52

Mushroom a écrit:ben on a ça

donc (sin(alpha-beta)/2)(ax-by) = 0
ssi ax-by=0 ou sin (bidule chouette) = sin 0

ahhh mais tu veux dire qu'a partir de l'a on peut s'arreter :id:

Ba ca veut dire que si le sin( ) est nul alors à Pi près l'intérieur est nul et donc alpha = bêta à Pi près... Donc on ne regarde que l'autre équation possible

Edit : Il est bien précisé que O, A et B ne sont pas alignés ce qui serait le cas si alpha = bêta + k Pi

par **Mushroom** » 11 Jan 2009, 16:01

bon merci beaucoup faut que j'ai les reflexe de passer d'une forme à une autre d'un complexe maintenant ^^

je repasse ce soir pour les 2 autres questions

Merci encore pour ton aide précieuse :)

par **Mushroom** » 11 Jan 2009, 22:16

Yop encore moi

pour la 3b) j'ai fait un truc mais bon je ne sais pas si on peut :/

alors M est barycentre donc

xMA+yMB=0
(en terme de vecteur)
xMA=-yMB

en longueur cela signifie que
xMA=yMB
yMB est non nul donc
xMA/yMB = 1

on a démontrer tout a l'heure que
ax-by = 0
ax/by= 1

xMA/yMB =ax/by
on supprime les x/y

MA/MB = a/b

CQFD

je réfléchis pour la derniere mais c'est pas gagné ^^'

par **Mushroom** » 15 Jan 2009, 17:42

je voudrais upper pour la question 4 ^^"

par **Mushroom** » 18 Jan 2009, 14:40

up encore pour la question 4

[DM-Nombre Complexe-Barycentre-Bissectrice]

[DM-Nombre Complexe-Barycentre-Bissectrice]

Qui est en ligne