Réduction d'un déterminant
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 20:25
par nico3004 » 30 Aoû 2010, 20:25
Bonsoir, il m'est également demandé de calculer le déterminant de cette matrice par réduction de son ordre et puis de résoudre l'équation :
(x 0 1 2)
(2 x 0 1) = 0
(1 2 x 0)
(0 1 2 x)
Pourriez-vous m'aider s'il vous plait, je ne comprends pas...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 20:41
par girdav » 30 Aoû 2010, 20:41
Bonjour,
que sais-tu sur les déterminants? Ici, on peut faire la manipulation

ce qui permet de mettre en facteur
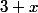
.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 20:56
par Dinozzo13 » 30 Aoû 2010, 20:56
Dis moi si j'ai faux Girdav, as-t-on :

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 20:58
par girdav » 30 Aoû 2010, 20:58
C'est correct (j'ai vu que tu as développé suivant la première ligne) et je pense que c'est ce qui est attendu. On en saura plus quand nico3004 reviendra.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 21:02
par Dinozzo13 » 30 Aoû 2010, 21:02
Merci de la confirmation, cela prouve que je maîtrise les bases du programme de 1re ES :ptdr:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 21:04
par girdav » 30 Aoû 2010, 21:04
Pour un futur MPSI (oui, j'ai regardé le profil), c'est presque la moindre des choses. :we: Je dis bien presque car il y a des trucs en ES que l'on ne voit pas en S (en tout cas pas à mon époque, qui n'est pas éloignée) : graphes, fonctions de deux variables et comme tu viens de le constater, les matrices et les déterminants.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 21:06
par Dinozzo13 » 30 Aoû 2010, 21:06
Oui en effet :++:
j'ai vu un peu les fonctions de deux variables ainsi que de les tracer et on voit pas grand chose dessus malheureusement en ES.
Par contre les graphes j'ai rien pigé :(
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 21:25
par nico3004 » 30 Aoû 2010, 21:25
c'est aussi ce que j'ai fait, mais après pour le résoudre... j'arrive à une équation :
x^4 - 2x² + 14x - 15 = 0
ce qui m'a l'air un peu complexe
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 21:29
par girdav » 30 Aoû 2010, 21:29
Bon, histoire de polluer un peu le fil, pour comprendre la formule de développement du déterminant (ici selon la première colonne), il faut des connaissances sur le groupe symétrique.
En fait le déterminant est une somme sur toutes les permutations (si Olympus passe par là...) de l'ensemble
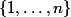
pour les matrices d'ordre

(sinon de
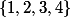
dans le cas qui nous intéresse). On décompose la somme en

sommes : on partitione le groupe symétrique en les ensembles
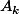
, où
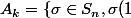=k\})
et on somme dessus.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 21:38
par girdav » 30 Aoû 2010, 21:38
Bon, je me lance dans le calcul :
 &= \begin{vmatrix}x&0&1&2\\<br />2&x&0&1\\<br />1&2&x&0\\<br />0&1&2&x<br />\end{vmatrix}\\<br />&=\begin{vmatrix}x+3&0&1&2\\<br />x+3&x&0&1\\<br />x+3&2&x&0\\<br />x+3&1&2&x<br />\end{vmatrix}\\<br />&=(x+3)\begin{vmatrix}1&0&1&2\\<br />1&x&0&1\\<br />1&2&x&0\\<br />1&1&2&x<br />\end{vmatrix}<br />\end{align})
puis on effectue

,

et

ce qui mène après développement à
 &=(x+3)\begin{vmatrix}1&0&1&2\\<br />0&x&-1&-1\\<br />0&2&x-1&-2\\<br />0&1&1&x-2<br />\end{vmatrix}\\<br />&=(x+3)<br />\begin{vmatrix}<br />x&-1&-1\\<br />2&x-1&-2\\<br />1&1&x-2<br />\end{vmatrix}<br />\end{align}.)
Je te laisse continuer.
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 21:38
par nico3004 » 30 Aoû 2010, 21:38
je ne suis plus :triste:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 21:42
par girdav » 30 Aoû 2010, 21:42
nico3004 a écrit:je ne suis plus :triste:
Pas la peine (pour l'instant) de tenir compte du message #9.
Je pense qu'il faut dans un premier temps faire du bricolage sur les ligne ou les colonnes de façon à faire apparaître un terme de premier degré en

en facteur. Ceci est dans l'optique d'obtenir les valeurs pour lesquelles le déterminant est nul.
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 21:45
par nico3004 » 30 Aoû 2010, 21:45
ok ok j'ai compris
et selon toi, est-ce qu'il y aurait encore moyen de simplifier la matrice 3 x 3 obtenue ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 21:55
par girdav » 30 Aoû 2010, 21:55
On doit pouvoir s'en sortir par la magouille

et

ce qui mène à :
&x+1&-2\\<br />1+x&-x+3&x-2<br />\end{vmatrix}\\<br />&= -\begin{vmatrix}<br />x^2-x+2&x+1\\<br />x+1&-x+3<br />\end{vmatrix}\\<br />&=-\begin{vmatrix}<br />x^2+3&4\\<br />x+1&-x+3<br />\end{vmatrix}\\<br />&=-\begin{vmatrix}<br />x^2+7&4\\<br />4&-x+3<br />\end{vmatrix}<br />\end{align})
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 22:01
par nico3004 » 30 Aoû 2010, 22:01
ok ! compris ! puis on arrive à (x+3)(-x^3+3x² - 7x + 5) = 0
saurais-tu comment trouver les racines du polynome du troisième degré ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Aoû 2010, 22:05
par Dinozzo13 » 30 Aoû 2010, 22:05
il y a une racine évidente pour ton polynôme de degré 3 : x'=1 ^^
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Aoû 2010, 22:06
par girdav » 30 Aoû 2010, 22:06
ll y a une méthode (due à Cardan) je crois mais ce n'est pas nécessaire ici puisque "par chance"

est racine.
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 22:06
par nico3004 » 30 Aoû 2010, 22:06
évidente évidente... comment fais-tu pour qu'elles te soient si évidentes ?
-
nico3004
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Aoû 2010, 20:13
-
 par nico3004 » 30 Aoû 2010, 22:09
par nico3004 » 30 Aoû 2010, 22:09
et en fait, c'est la seule solution de l'équation finalement
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Aoû 2010, 22:12
par benekire2 » 30 Aoû 2010, 22:12
Dinozzo13 a écrit:Par contre les graphes j'ai rien pigé

C'est cool je trouve les graphes, cela dit, y voient pas grand chose dessus non plus. Après ils voient les matrices, mais les déterminants je ne crois pas. . .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
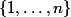 pour les matrices d'ordre
pour les matrices d'ordre  (sinon de
(sinon de 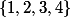 dans le cas qui nous intéresse). On décompose la somme en
dans le cas qui nous intéresse). On décompose la somme en  sommes : on partitione le groupe symétrique en les ensembles
sommes : on partitione le groupe symétrique en les ensembles 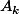 , où
, où 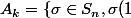=k\}) et on somme dessus.
et on somme dessus.