Déterminant
17 messages
- Page 1 sur 1
Le déterminant d'un systeme de deux equations à deux inconnues???
Par exemple prenons le systeme suivant:
ax+by=g
cx+dy=f
le determinant est egale à:
ad-bc
si il est different de 0 alors, le systeme admet une unique solution, un unique couple (x,y).
si il est nul, alors on a deux possibilités:
soit le systeme n'admet aucune solution.
soit il admet une infinintés de solutions.
alors dans ce cas (determinant=0) on ne resout pas le systeme comme d'habitude. mais on met les deux equations du systeme:
y=rx+g
y=rx+g'.
(si aucune erreur n'a ete commise, si le determinant est nul les deux coefficient directeur sont identique).
on est en presence de deux droites paralleles ici (meme coeff directeur).
si g est different de g', le systeme admet aucune solutions. les droites sont strictement parallele.
si g=g' alors dans ce cas le systeme admet une infinites de solutions. les droite sont confondus. Le systeme admettra ici comme solutions tous les couples de la forme (x,rx+g).
Voila, vu qu'on est dans la section lycée, je suppose que ta question porté la dessus.
Le pourquoi du comment, ben disons que 2 droites sont paralleles si et seulement si ce determinant est nul.
Apres l'etude du determinant se fait en supérieur, lors de l'etude des systemes lineaires en algebres lineaires notemment.
Pour un systeme à trois equations à trois inconnues, il existe un determinant mais dont la formule est assez complique.
je sais pas si j'ai repondu a la question
edit: j'ai pas vu ton deuxieme message avant de la redaction de ce message
Par exemple prenons le systeme suivant:
ax+by=g
cx+dy=f
le determinant est egale à:
ad-bc
si il est different de 0 alors, le systeme admet une unique solution, un unique couple (x,y).
si il est nul, alors on a deux possibilités:
soit le systeme n'admet aucune solution.
soit il admet une infinintés de solutions.
alors dans ce cas (determinant=0) on ne resout pas le systeme comme d'habitude. mais on met les deux equations du systeme:
y=rx+g
y=rx+g'.
(si aucune erreur n'a ete commise, si le determinant est nul les deux coefficient directeur sont identique).
on est en presence de deux droites paralleles ici (meme coeff directeur).
si g est different de g', le systeme admet aucune solutions. les droites sont strictement parallele.
si g=g' alors dans ce cas le systeme admet une infinites de solutions. les droite sont confondus. Le systeme admettra ici comme solutions tous les couples de la forme (x,rx+g).
Voila, vu qu'on est dans la section lycée, je suppose que ta question porté la dessus.
Le pourquoi du comment, ben disons que 2 droites sont paralleles si et seulement si ce determinant est nul.
Apres l'etude du determinant se fait en supérieur, lors de l'etude des systemes lineaires en algebres lineaires notemment.
Pour un systeme à trois equations à trois inconnues, il existe un determinant mais dont la formule est assez complique.
je sais pas si j'ai repondu a la question
edit: j'ai pas vu ton deuxieme message avant de la redaction de ce message
salut J-R !
je n'ai jamais fait de déterminant, mais ma prof de seconde nous faisait vérifier l'existence et l'unicité de la solution en prenant les vecteurs directeurs des droites de ton systeme (d'équation Ax + By = C)
en fait si je prend
) et
et
)
on vérifie que I et J ne sont pas colinéaires en appliquant la relation u(a;b) et v(a';b') sont colinéaires ssi ab' - a'b = 0
EDit : grillé antho :ptdr:
je n'ai jamais fait de déterminant, mais ma prof de seconde nous faisait vérifier l'existence et l'unicité de la solution en prenant les vecteurs directeurs des droites de ton systeme (d'équation Ax + By = C)
en fait si je prend
on vérifie que I et J ne sont pas colinéaires en appliquant la relation u(a;b) et v(a';b') sont colinéaires ssi ab' - a'b = 0
EDit : grillé antho :ptdr:
si nickel c'est bon (j'avais déjà regardé sur des cours de sup mais il mélangeait cela à des matrices et je ne comprenait pas trop) j'ai bien compris en faisant allusion à la géométrie (on voir mieux les choses)) 
donc pour mon système: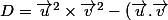^2)
dans mon énocé et
et  sont non colinéaires donc grace à cauchy schwarz (qui est donc strcit) le déterminant n'est pas nul.
sont non colinéaires donc grace à cauchy schwarz (qui est donc strcit) le déterminant n'est pas nul.
donc pour mon système:
dans mon énocé
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
