Prouver l'existence d'une Limite

[houda 20]

alors dans la définition
tu vas prouver à quelqu'un que
s'il prend n'importe quel nombre réel positif, alors il va trouvé un delta tel que(...........)
c'est ça
c'est comme
s'il prend n'importe quelle boite des boites devant lui il va trouver un cadeau dedans

comme tu dois lui montrer tout les cadeaux en ouvrant les boites

tu dois nous montrer le delta qui vérifie(.......) si on prend n'importe quel epsilon 'le epsilon traine sur tout R+'

tu as compris ça?????????

[houda 20]

c'est pas clair????

[houda 20]

c'étais pour que tu comprenne que ce que tu dois chercher

[houda 20]

alors, je continue?

[houda 20]

merci infiniment.........

[Tommy1991]

jusque là ca va :) (j'étais sorti 10 min c'est pour ca que j'ai pris un peu de temps)

[houda 20]

d'accord, d'accord
puisque tu as compris c'est très bien
donc ton problème est de chercher la valeur de delta et non pas de epsilon
on est d'accord sur ça

[Tommy1991]

ouep par contre je ne vois pas encore comment y arriver

[houda 20]

pas par pas, il ne reste pas bcp tant que tu as compris que ce que tu veux c'est trèèèèèèèèèèèèès trèèèèèèèès bien

[houda 20]

notre fugitif "delta" monsieur " le détective Tommy1991" se caractérise par
si 0 < | x - p | < ;) alors | f(x) - L | <
sachant qu'on connait les les mon sieurs p et L....
C'EST BON JUSQu'à là....

[houda 20]

et madame f(x) encore......

[houda 20]

le epsilon, je le connait ou non?????????

[Tommy1991]

euh non je crois pas tout ce qu'on sais d'epsilon c'est qu'il est positif

[houda 20]

mais tu cherche delta pour tout epsilon
i.e tu vas me montrer le delta en sachant epsilon
comme l'exemple précédent, je vais prendre une boite quelconque et tu vas me montrer le cadeaux
c'est bien pareil, quand je vais prendre un epsilon positif, tu vas me donner le delta
tu as compris ça.....
i.e en cherchant ton delta, on aurai déjà fixé un certain epsilon positif

en résumé, on prend un epsilon quelconque te on trouvera le delta

d'ailleurs c'est ça ce que tu nous a dit, prend n'importe quel epsilon, et vous allez retrouver un delta qui vérifie(.....le reste de la proposition........)

c'est bon pour ça?????

[houda 20]

alors tu vas dire
si epsilon est un entier positif réel quelconque, alors on aura......................'ça va venir'

bon, Tommy1991, je vais me tirer pour dix minutes pour ma prière et je reviendrai
à ce temp là, résume tout ce que nous sommes d'accord sur, et écrit le moi
que ce que tu as compris.......

[Tommy1991]

on aura un delta entier positif également.

Résumé :

Pour tout 0 < ;) il existe un 0 < ;) de telle manière que :

0 < | x - p | < ;) => | f(x) - L | < ;)

[houda 20]

salut
bon, c'est bien
maintenant, en cherchant ton delta, tu as besoin de commencé d'un endroit précis
un endroit qui est bien une relation de choses que tu connais déjà ,d'ou tu pourras démarrer pour arriver.
là, quelle est l'endroit duquel tu vas commencé???????

[houda 20]

on va commencé de
| f(x) - L | puisque tu as tout les données
et on veut arriver à
| x - p | < ;) (le delta dépend de epsilon bien sur, lorqu'on change epsilon, le delta peut changer)..........

[Ben314]

Je sais pas si ca t'aidera à comprendre, mais cette 'fameuse' définition :

Pour tout 0 | f(x) - L | <

elle dit en langage mathématique que :
"On peut rendre f(x) aussi proche de L que l'on veut à condition d'avoir pris x suffisement proche de p"
Cela correspond assez bien à l'idée intuitive de limite.

Pour la "rédaction", si ça te dérange de savoir si on "connait" ou pas le je te propose (au début) la rédaction suivante :

On fixe un (dans ma tête, ça veut dire je le connait : c'est 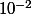ou bien )
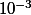Pour ce là, je vais cherche un tel que : | f(x) - L | < <= 0 < | x - p | <
(je l'écrit exprés à l'envers car dans les calculs on écrit en premier | f(x) - L | < puis on cherche une (ou des) conditions pour que ce soit vrai).
Une fois que l'on a trouvé le on peut écrire :

Or le que l'on a pris au début est quelconque donc cela signifie que c'est vrai pour tout .

A la limite, si tu n'as jamais fait ce genre d'exos, je sais pas si c'est pas malin de commencer avec un "vrai ", c'est à dire essayer de trouver un
tel que | f(x) - L | <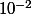 <= 0 < | x - p | <
puis idem avec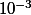 jusqu'à ce que tu te rende compte... que c'est ridicule et qu'il est plus rapide de l'écrire dés le début avec un ...

[Tommy1991]

ok, jusque là ca va, je vais aller me coucher car je suis exténué et reprendrai ca demain.

Merci pour ton aide en tout cas :)