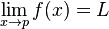Prouver l'existence d'une Limite

[Tommy1991]

Bonjour,

Je suis nouveau ici, je suis actuellement à l'université de Maastricht étudiant les maths appliqués et l'intelligence artificiel. Le problème étant que je suis tombé malade et ai donc raté beaucoup de cours (plus de la moitié). Et mes vagues souvenirs en math ne me permettent pas de combler toutes les interrogations que j'ai aujourd'hui. Etant donné que mon examen approche a grand pas j'ai décidé de prendre le taureau par les cornes et de me battre pour cette session plutôt que de la rater et attendre la suivante.

Considérez la fonction f(x) définie dans l'interval I = (0, +00) :



1°) Existe-t-il une limite de f(x) lorsque x tend vers 3? Si oui calculer la (1/6 je dirais mais je ne suis pas sûr).

2°) f(x) est-elle continue sur l'interval I ? (C'est évident que non mais je ne sais pas le prouver)

3°) Si f(x) n'est pas continue, vous pouvez changer la valeur de f(x) au point x = 3 pour que la fonction devienne continue sur l'interval I ?

Ce n'est peut-être pas très clair étant donné que c'est traduit de l'anglais.

Merci d'avance.

Cordialement Tommy1991.

[Edit] L'idéal serait de pas me résoudre l'exercice mais plutôt me faire comprendre comment cela fonctionne

[Zweig]

Salut,

1) Simplifie de sorte qu'on n'obtienne plus une forme indéterminée du type "0/0" lorsque l'on veut calculer la limite. Tu trouves que la limite est

2) Reviens à la définition de la continuité : une fonction f est continue en a si et seulement si

Par hypothèse, . Or d'après 1), , donc ... ?

3) C'est direct si tu as bien compris le raisonnement du 2).

[Tommy1991]

Tout d'abord merci pour tes rapides réponses, mais pour le numéros 1 il faut prouver qu'elle existe le prof fait ca avec la définition d'une limite :



Pour tout > 0 il existe > 0 de tel manière que 0 < | x - p | < implique
| f(x) - L | < (chose que je ne comprends absolument pas)

Je ne sais pas si calculer suffit à prouver son existence.


--------------------------

Pour la question 3 je pense que c'est f(x) = 3 if x = 3

Cordialement Tommy1991

[houda 20]

salut
normalement la calculer prouve son existence, mais dé fois on nous oblige d'appliquer la définition pour nous entrainer.
pour une fonction qui a une limite, c'est facile d'appliquer la définition
voilà comment tu fais
prends l'inégalité
| f(x) - L | < ;)
remplace ta fonction et la limite et essaye de majorer | x - p | et tu trouveras ton delta en fonction de ;)
c'est pas difficile pour ton cas je pense
bonne chance
pour la 3eme question
tu prends f(3)=1/6 tout simplement

[Tommy1991]

j'arrive à réduire ceci :

| f(x) - L | < ;)

à ceci :

| - (x-3) | < ;)

ce qui donne ceci (je crois) | x - 3 | = | x - p | < ;)

maintenant je ne sais pas quoi faire pour la suite.

[houda 20]

eh bien tu as finis
prends ton delta=;)
et c'est tout
le problème est de trouver delta tel que si
| x - p | < delta alors tu aurais la deuxième inégalité, i.e
| f(x) - L | < ;)
lorsqu'on dit quelque soit epsilon, on trouve delta tel que.............
ça veut dire
que si on prend epsilon positif, n'importe lequel on trouve delta tel que si | x - p | < delta alors | f(x) - L | < ;)
si tu as | x - 3 | < epsilon alors tu arriveras à | f(x) - 1/6 | < ;)
si tu as bien majoré tu retrouveras | f(x) - 1/6 | < ;) en démarrant de | x - 3 | < epsilon

[Tommy1991]

Donc ce que j'ai écrit suffit à prouver qu'il existe une limite ? Je comprends pas vraiment ce que tu veux dire par majorer.

En tout cas merci beaucoup pour ton aide.

Cordialement Tommy1991

[houda 20]

d'accord, écris moi comment t'es arrivé au résultat

[Tommy1991]

|f(x) - L| < ;)

|1/(x + 3) - 1/6| < ;)

|6 - (x - 3)| < ;)

|6 - 3 - x | < ;)

|3 - x | < ;)

|- (x - 3)| < ;)

Ici je suis pas certain :

|x - 3| < ;)


Puis |x - 3| = |x - p| donc

0 < |x - 3| < ;)

Et

0 < |x - 3| < ;)

[houda 20]

voilà, tu prends ton |f(x) - L| , tu la majore en cherchant un majorant qui est en fonction de | x - p | et quand tu le retrouve tu fais " majorant< ;)" et donc tu auras
"| x - p |< quelque chose de ;)" par conséquent
tu écris

quelque soit ;), il existe delta=quelque chose de ;), tel que si
| x - p |< quelque chose de ;) alors on aura |f(x) - L|< majorant< ;)
"majorant" tu ne l'écrit pas, je te l'ai écrit pour que tu comprends pourquoi je cherche à majorer, c'est bon, c'est clair maintenant???

[houda 20]

ça c'est la méthode qu'on suit habituellement
pour tes calculs, je n'ai pas vérifié

[Tommy1991]

je dois pas trouver une valeur pour ;) et ;) ??? Car j'ai l'impression qu'il manque quelque chose moi comme ca j'ai juste modifier la forme de leur équation c'est tout, j'ai rien fait d'autre ca me semble trop "simple" ^^.

[houda 20]

ça veut dire quoi tout ça
voilà
pour tout epsilon surtout "on veut pour le epsilon qui est très très petit", i.e que f(x) est si proche de la limite L "c'est ça ce qui veut dire" |f(x) - L|< ;) donne que
-;)+L < f(x) < ;)+L" on trouveras delta tel que pour tout les x compris entre p-delte et p+delta tu aurai tes f(x) sont proches de ta limite
c'est ça f(x) tend vers L
donc,surtout pour tout epsilon trooooooooooooooooooooooooop 'petit ce qui va nous donner que f(x) sera trooooooooooooooooooooooooooop proche de L quand x s'approche de p', on trouveras surement un delta, i.e un voisinage de p (car tu dis f(x) entd vers L quand x tend vers p) tel que les images de tout ces x dans le voisinage sont bien proches de L.

[houda 20]

ça veut dire que tu ne pm'as pas encore compris
en essayons de prouver cette définition, il faut faire quoi?

[Tommy1991]

je comprends effectivement pas du tout ce que tu as écris :S

[houda 20]

réponds moi avant.......

[Tommy1991]

je ne sais pas la réponse

[houda 20]

alors dis moi, pour prouver tout ce bla bla, tu cherche à prouver quoi????????

[houda 20]

d'accord, réecris moi la définition

[houda 20]

vas y.........j'attends