Endomorphisme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ludo56
- Membre Relatif
- Messages: 338
- Enregistré le: 16 Juil 2007, 11:49
-
 par ludo56 » 22 Nov 2009, 10:34
par ludo56 » 22 Nov 2009, 10:34
Bonjour,
soit f

L(E)
soit E = somme directe des
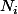
avec
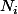
sont les sous-espaces caractéristiques de f
On pose

i,

x

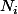
, d(x) =

x.
d est-il un endomorphisme de E ? ie est il linéaire?
merci!
 par alavacommejetepousse » 22 Nov 2009, 11:09
par alavacommejetepousse » 22 Nov 2009, 11:09
bonjour
question mal posée
a priori d n est défini que sur la réunion des Ni
en fait il existe un unique endo d de E tel que sa restriction à chaque Ni soit di un endomorphisme de Ni imposé
donc oui
-
ludo56
- Membre Relatif
- Messages: 338
- Enregistré le: 16 Juil 2007, 11:49
-
 par ludo56 » 22 Nov 2009, 11:50
par ludo56 » 22 Nov 2009, 11:50
donc d'après ce que j'ai compris, il faudrait poser :
d =

°

+ ... +
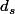
°
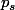
avec

les projecteurs (endomorphismes de E) qui envoie x

E sur son projeté sur
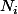
et
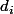
l'homothétie (endomorphisme de
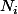
) de rapport

.
c'est ça ?
 par alavacommejetepousse » 22 Nov 2009, 11:57
par alavacommejetepousse » 22 Nov 2009, 11:57
moui mais non car la composition n'a pas de sens entre un endo de E et de Ni
en revanche on peut l 'écrire pour x = sigma(x(i) )
d(x) = sigma lambda (i) x(i)
-
ludo56
- Membre Relatif
- Messages: 338
- Enregistré le: 16 Juil 2007, 11:49
-
 par ludo56 » 22 Nov 2009, 12:05
par ludo56 » 22 Nov 2009, 12:05
je ne comprends pas pourquoi ça n'a pas de sens car quand on applique

à x

E ça l'envoie dans
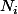
puis on applique ceci à
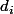
qui l'envoie dans
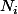
...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2009, 12:30
par Ben314 » 22 Nov 2009, 12:30
La composé d_i o p_i n'a de sens que si l'espace d'arrivé de p_i est contenu dans celui de départ.
si tu considère que les projection p_i sont des endomorphismes de E dans E alors tu n'as pas le droit de faire la composée.
Par contre tu peut voir les p_i comme des morphismes de E dans N_i et dans ce cas tu as le droit de les composer.
La différence entre les deux point de vue peut parraitre con-con, mais si tu réfléchi un peu, dans le premier cas la (une) matrice associée à p_i sera une matrice carré et dans le second cas une matrice non carré et là on voit que la différence est importante...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
LoLLoLLoL
- Membre Naturel
- Messages: 40
- Enregistré le: 18 Nov 2009, 13:18
-
 par LoLLoLLoL » 22 Nov 2009, 12:35
par LoLLoLLoL » 22 Nov 2009, 12:35
Qu'appelle tu sous espace caracteristique ? ( ie sous espace propres ?)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2009, 12:38
par Ben314 » 22 Nov 2009, 12:38
A mon avis, il vaut mieux suivre le conseil de alavacommejetepousse
et écrire simplement que :
f(x)=\lambda_1.x_1+\lambda_2.x_2+...\lambda_s.x_s
lorsque x=x_1+x_2+...x_s est la décomposition de x suivant les espaces N_i
ca évite toute ambigüité sur qui sont les p_i (E->E ou E-> N_i ?).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ludo56
- Membre Relatif
- Messages: 338
- Enregistré le: 16 Juil 2007, 11:49
-
 par ludo56 » 22 Nov 2009, 12:53
par ludo56 » 22 Nov 2009, 12:53
LoLLoLLoL a écrit:Qu'appelle tu sous espace caracteristique ? ( ie sous espace propres ?)
le sous-espace caractéristique de

est Ker
^\alpha)
avec \alpha la multiplicité de \lambda.
merci pour toutes ces précisions !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 22 Nov 2009, 12:54
par yos » 22 Nov 2009, 12:54
En quoi la question est-elle mal posée?
Un endomorphisme peut être défini de diverses façons : par l'image d'une base, ou comme ici, par sa restriction à chaque terme d'une somme directe.
Ce qui est bizarre, je vous l'accorde, c'est de demander ensuite si c'est un endomorphisme.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2009, 12:59
par Ben314 » 22 Nov 2009, 12:59
tout à fait thierry !!!!
(j'en déduit qu'il en est sans doute au début de l'alg. linéaire. et que ce ne doit pas être complètement clair que l'on peut définir les endomorphismes de différentes façon...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 22 Nov 2009, 14:06
par yos » 22 Nov 2009, 14:06
Les s.e.c., c'est pas tout à fait le début de l'algèbre linéaire. Le fait qu'ils soient en somme directe nécessite le théorème de décomposition des noyaux.
La décomposition de d en combinaison linéaire de projecteurs que propose ludo56 est tout de même pertinente.
L'écriture
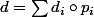
vaut bien
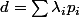
.
 par alavacommejetepousse » 22 Nov 2009, 16:40
par alavacommejetepousse » 22 Nov 2009, 16:40
yos a écrit:En quoi la question est-elle mal posée?
Un endomorphisme peut être défini de diverses façons : par l'image d'une base, ou comme ici, par sa restriction à chaque terme d'une somme directe.
Ce qui est bizarre, je vous l'accorde, c'est de demander ensuite si c'est un endomorphisme.
bonsoir
on définit a priori
d uniquement sur l union des Ni donc ce n'est même pas une application de E dans E
la question bien posée serait : montrer qu'il existe un unique endo de e dont la restriction à chaque Ni est ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités