[Exercice simple pour experimenter mais trés interresant ]
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
mito94
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Juin 2009, 08:03
-
 par mito94 » 18 Oct 2009, 07:32
par mito94 » 18 Oct 2009, 07:32
Bonjour ce matin je suis tomber sur un exo de spé maths auxquel j'ai eu beaucoup de mal mais je l'ai trouver trés interessant meme si il va vous paraitre "simple". voici l'enoncé : :marteau: demontrer que :
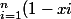\geq 1-\bigsum_{i=1}^{n} xi)
pour xi appartient a [[0;1]] et n appartient a
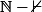
Personnellement je n'ai pas réussit :p du tout meme :zen:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 18 Oct 2009, 08:16
par fatal_error » 18 Oct 2009, 08:16
salut,
pe par récurrence :
au rang 1 :
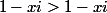
au rang n+1 :
\bigprod_{k=1}^{n} (1-x_i) = a - ax_{n+1})
avec
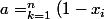)
et
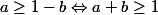
avec
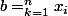
on cherche a montrer
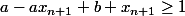
Or
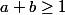
par récurrence au niveau n.
et
 \ge 0)
car
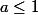
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités