Inégalités
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Xavier12
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Juil 2009, 16:49
-
 par Xavier12 » 29 Aoû 2009, 13:46
par Xavier12 » 29 Aoû 2009, 13:46
Salut, quelqu'un pourrait il me dire quel est le truc a voir ou a savoir afin de demontrer cette inégalité ?
^n)
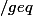
1-nx.
Merci.
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 29 Aoû 2009, 14:04
par egan » 29 Aoû 2009, 14:04
Soit tu étudies le signe de la différence, en te servant de la loi du binôme de Newton, ce qui me paraît pas très concluant à première vue; soit tu dois pouvoir t'en tirer à coup de récurence.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 29 Aoû 2009, 14:05
par le_fabien » 29 Aoû 2009, 14:05
Bonjour,
et bien il faut connaitre les développements limités mais c'est pas du niveau lycée.
-
Xavier12
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Juil 2009, 16:49
-
 par Xavier12 » 29 Aoû 2009, 14:11
par Xavier12 » 29 Aoû 2009, 14:11
Mais le binome de Newton ce n'est pas qu'avec
^n)
?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 29 Aoû 2009, 14:33
par Ericovitchi » 29 Aoû 2009, 14:33
j'aime bien le "qu'avec"
Ne te sembles t-il pas que
^n)
c'est
^n)
avec a=1 et b=-x ?
-
Xavier12
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Juil 2009, 16:49
-
 par Xavier12 » 29 Aoû 2009, 14:45
par Xavier12 » 29 Aoû 2009, 14:45
hum effectivement, j'ai pas l'impression que je vais faire des ravages en mathématiques :triste: . Merci beaucoup.
-
Xavier12
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Juil 2009, 16:49
-
 par Xavier12 » 29 Aoû 2009, 15:05
par Xavier12 » 29 Aoû 2009, 15:05
Veuillez m'excuser mais je n'arrive pas à trouver le signe ; la formule du binome de Newton me complique les calculs car je me retrouve avec du

"

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 29 Aoû 2009, 15:13
par Ericovitchi » 29 Aoû 2009, 15:13
Effectivement :
^n=\sum_{k=0}^n {n \choose k} (-x)^k = 1-nx+\frac{n(n+1)}{2} x^2+ ... + (-1)^{n}x^{n})
Essayes de plutôt étudier la fonction
=(1-x)^n+nx-1)
en regardant le signe de la dérivée.
-
Xavier12
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Juil 2009, 16:49
-
 par Xavier12 » 29 Aoû 2009, 15:24
par Xavier12 » 29 Aoû 2009, 15:24

*
^k)
= 1-nx ? quand k=0.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 29 Aoû 2009, 15:32
par Ericovitchi » 29 Aoû 2009, 15:32
et en fait elle n'a pas l'air toujours vraie ton inégalité. Tu veux la démontrer quelque soit x et n ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 29 Aoû 2009, 15:39
par Ericovitchi » 29 Aoû 2009, 15:39
= 1-nx ? quand k=0.
pas tout à fait, le 1 est obtenu pour k=0, le -nx pour k=1, etc... . tu as du mal à visualiser les premiers termes ?
Prenons k = 0
^0 = 1)
Prenons k = 1
^1 = -nx)
Prenons k = 2
^2 = \frac{n(n+1)x^2}{2})
Mais étudies plutôt la fonction
=(1-x)^n+nx-1)
on montre facilement que la dérivée est positive et donc que la fonction est croissante (du moins tant que x n'est pas trop grand).
Par contre l'inégalité n'est plus valable pour les x grand pour les n impairs (la fonction tend vers - l'infini pour les n impairs).
-
Xavier12
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Juil 2009, 16:49
-
 par Xavier12 » 30 Aoû 2009, 11:47
par Xavier12 » 30 Aoû 2009, 11:47
Veuillez excuser mon retard, je tiens a vous remercier Ericovitchi ainsi qu'aux autres m'ayant consacrer du temps ; j'ai reussi grace a votre precieuse aide a terminer cet exercice . :happy2:
A Bientot.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
^n)
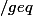 1-nx.
1-nx.