Inégalité - n variables
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 26 Juil 2009, 12:19
par Zweig » 26 Juil 2009, 12:19
Salut,
Une autre inégalité que j'ai inventée.
Soient

des réels strictement positifs et

un entier naturel. Montrer l'inégalité suivante :
[CENTER]

[/CENTER]
Je rappelle que

est le coefficient binominal.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 26 Juil 2009, 12:26
par Zweig » 26 Juil 2009, 12:26
Je conçois qu'elle est moche :we: Je tâcherai d'en faire des plus élégantes la prochaine fois ...
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 26 Juil 2009, 12:26
par Maks » 26 Juil 2009, 12:26
On a même pas encore eu la réponse de l'autre !! :cry:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 26 Juil 2009, 12:28
par Zweig » 26 Juil 2009, 12:28
Ah, tu veux la réponse pour l'autre ?
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 26 Juil 2009, 12:44
par Maks » 26 Juil 2009, 12:44
Ouais, je veux bien. (Mets en caché si tu veux).
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Juil 2009, 15:24
par Zweig » 27 Juil 2009, 15:24
Up :++: mmmmmmmmmmmmmmmmmmmmmmmmmmmmm
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 31 Juil 2009, 21:12
par Zweig » 31 Juil 2009, 21:12
Bon, comme ça n'inspire pas grand monde

, je poste la solution (
ici) lorsque
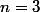
. Le cas général se résout sensiblement de la même manière, en utilisant le cas général de l'inégalité arithmético-géométrique.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
 [/CENTER]
[/CENTER] [/CENTER]
[/CENTER]