Changement de variable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 23 Juin 2009, 14:32
par Azuriel » 23 Juin 2009, 14:32
Bonjour,
Je viens solliciter votre aide car j'ai de gros doute sur un changement de variable a faire lors d'un exercice...
Vous n'avez pas besoin de chercher pourquoi ni de connaitre u car l'aide que je vous demande porte uniquement sur la manipulation mathématique.
En effet comment ma grosse expression présentant des dérivées partielles et des integrales se transforment quand je fais le changement de variable par rapport a la premiere variable s -> s-t (il me semble que c'est ça).
La question se trouve de toute sur ce scan. En dessous de la grosse expression ( (3) ) se trouve la consigne qui me fait douter et me pose problème.
[CENTER]
http://img200.imageshack.us/img200/5240/changementdevariable.jpg [/CENTER]
Merci d'avance pour votre aide

.
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 24 Juin 2009, 08:53
par Azuriel » 24 Juin 2009, 08:53
Je précise juste pour ceux a qui ça ferait peur de ne pas se soucier des E représentant l'esperance. Car je les appliques en fait plus tard. J'aimerai comprendre ce que me donne le changement de variable juste avec les intégrales.
Merci de m'aider...
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 24 Juin 2009, 09:13
par uztop » 24 Juin 2009, 09:13
Bonjour,
oui, c'est un simple changement de variable (même si l'expression est horrible).
Donc, il faut voir ce que deviennent les bornes de l'intégrale qui dépend de

et ce que devient le
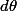
après le changement de variable.
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 24 Juin 2009, 09:28
par Azuriel » 24 Juin 2009, 09:28
Merci de la réponse.
Mais de la façon dont s'est posé là, t est une constante non et c'est s la variable ? Car je ne peux pas avoir s et t qui bouge en meme temps...
Et pourtant d'apres les question d'apres je devrais réussir a faire apparaitre des dérivée par rapport a t...et une fonction u dependant de t...
C'est ça qui m'embrouille. Personne pourrait m'éclairer ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 24 Juin 2009, 09:32
par uztop » 24 Juin 2009, 09:32
non s est une constante (c'est la borne de l'intégrale de départ); t est la variable
Il faut donc exprimer

en fonction de
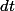
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 24 Juin 2009, 09:41
par Azuriel » 24 Juin 2009, 09:41
D'accord. Mais ce qui me parait bizarre c'est qu'on égalise donc une constante (phi(s, X, Y) ) a une fonction u(t-s, X, Y) qui varie par définition....
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 24 Juin 2009, 09:48
par uztop » 24 Juin 2009, 09:48
non, tu n'égalises pas (phi(s, X, Y) ) à u(t-s, X, Y) mais à l'intégrale de u par rapport à la variable d'intégration t; après intégration le résultat ne dépend plus de t.
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 24 Juin 2009, 09:51
par Azuriel » 24 Juin 2009, 09:51
Ah bon ? C'est sans doute cela qui me perturbait car d'apres mon scan, il égalisait les fonctions et pas les integrales des fonctions et donc ça paraissait bizarre.
Mais donc pour le premier terme par exemple, E (phi(0,Xo,Yo) ) ça devient E (u(t,Xo,Yo)) ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 24 Juin 2009, 10:02
par uztop » 24 Juin 2009, 10:02
en fait le terme constant n'a pas beaucoup d'importance; il devient u(-s,Xo,Yo) puisque t=0 dans phi(0,Xo,Yo) mais ce qui compte vraiment c'est les intégrales.
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 24 Juin 2009, 10:13
par Azuriel » 24 Juin 2009, 10:13
D'accord. Merci en tout cas d'avoir lever une bonne ambiguité.
Je vais regarder ça. Si j'ai un problème je vous en ferait part.
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 24 Juin 2009, 14:19
par Azuriel » 24 Juin 2009, 14:19
Euh mon changement de variable c'est theta donne t-s ou l'inverse ?
Et sinon j'ai dtheta=dt et mes bornes deviennent "de -s à 0" ??
Je suis encore embrouillé quand meme par égaliser un nombre phi(s,x,y) et une fonction u(t-s, x, y).
Peut on me preciser dans quel sens se fait le changement de variable dans mes integrales car là je suis perdu dans le sens...
Merci d'avance.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
