Fonction holomorphe

[Azuriel]

Bonjour !

Je debute tout juste dans mon apprentissage des fonction holomorphe et je bloque sur une question...

On me demande de montrer que la fonction fs qui va de Omega dans C et telle que fs(z)=1/z²+1)^s est holomorphe sur Omega avec s complexe et Omega definit comme l'ouvert obtenu en retirant au demi plan Im(s)>-1 la demi droite [i, i*infini[ (a noter que c'est un ouvert connexe car étoilé par rapport à tout point du segment ]-i,i[.

Alors là ce que je dois faire c'est de prendre un zo appartenant a Omega et montré qu'en son voisinage, fs(z) est developpable en serie entiere c'est ça ? Le probleme vient du fait que je ne sais pas comment gérer la puissance s complexe (l'énoncé précise qu'on utilise la détermination principale du logarithme mais je ne la connais pas et on me dit juste qu'avec cette determination on a |z^s|<=exp(Pi*|Im(s)| * |z|^Re(s)).

Merci d'avance pour votre aide.

[Arkhnor]

Salut.

La détermination principale du logarithme, c'est la fonction définie sur l'ouvert C\ R-, par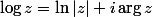 , avec l'argument à valeurs dans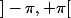
Elle est holomorphe dans cet ouvert (c'est du cours).

Ensuite, on définit les fonctions puissances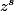 par . Elles sont définies là où le log est défini, et elles y sont holomorphes, comme composées de fonctions holomorphes. (le logarithme et l'exponentielle)

Ensuite, pour déterminer le domaine de définition de ta fonction, et savoir si elle y est holomorphe, c'est comme d'habitude, c'est une composée de fonctions holomorphes, on vérifie si on peut composer et on applique les théorèmes ...

(Si tu veux montrer qu'une fonction est holomorphe, tu peux simplement montrer qu'elle est C-dérivable, pas la peine de montrer qu'elle est développable en série entière, c'est automatique si elle est C-dérivable.
D'ailleurs, c'est les définitions, f est holomorphe sur un ouvert si elle est C-dérivable en tout point de l'ouvert, f est analytique sur un ouvert si elle est développable en série entière en tout point, et on a un théorème affirmant l'équivalence des deux notions)

[Azuriel]

Merci pour cette réponse si détaillé et rapide.

Je ne savais pas qu'une fonction C dérivable impliquait que la fonction était analytique. Tu connaitrais un lien vers une page d'un cours démontrant cela ? (juste par curiosité et comprendre le pourquoi du comment).

Merci pour la précision sur le log complexe.

Enfin le probleme reste maintenant de savoir comment montrer qu'une fonction est C derivable ? Il suffit de montrer qu'en tout point zo de Omega on a la limite du taux d'accroissement qui a une limite ? Ou existe t'il des méthodes plus faciles a mettre en oeuvre.

Et ici, le plus simple est de montrer qu'elle est developpable en serie entiere autour de tout point ou qu'elle est C derivable en tout point de Omega ?

[Azuriel]

Est ce que le developpement en serie entiere qu'on avait effectué avec s réel pour (1+z)^s peut s'appliquer avec s complexe ? Et ainsi demontrer sur quel domaine de C (1+z)^s est holomorphe pour ensuite appliquer des composés pour demontrer que 1/(1+z)^s est holomorphe sur Omega.

Ce qui me gene c'est que dans mon cours on me dit que (1+z)^s est holomorphe que sur D(0,1-) or cela m'empeche d'aboutir a mon resultat en composant avec z² (holomorphe sur C), puis 1/z (holomorphe sur C\{0}).

[Arkhnor]

J'ai rectifié mon message initial, la détermination principale du logarithme est définie sur C\R- (si on l'avait définie sur C\R+, on aurait pris l'argument à valeurs dans )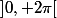

Sur ce site, il y a un bon poly d'analyse complexe : Lien
Le résultat dont je t'ai parlé repose sur la formule intégrale de Cauchy.

Je te conseille aussi Analyse réelle et complexe de Rudin, ainsi que Calcul Infinitésimal de Dieudonné.

Ensuite, dans ton cas, on a par définition
Cette expression est donc définie dès que est défini, c'est à dire quand 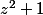est dans C\R-.

Une fois déterminé l'ensemble de définition (l'ensemble Oméga de ton énoncé est contenu dans celui-ci), l'holomorphie se déduit des théorèmes de composition. Il n'y a donc pas besoin de revenir aux définitions.

Une remarque, f est C-dérivable en z0 si existe. La valeur de la limite est appelé le nombre dérivé de f en z0 (c'est comme pour le cas réel, sauf que là on a beaucoup de résultats étonnants comme conséquence de cette définition).

[Azuriel]

Une fois déterminé l'ensemble de définition (l'ensemble Oméga de ton énoncé est contenu dans celui-ci), l'holomorphie se déduit des théorèmes de composition. Il n'y a donc pas besoin de revenir aux définitions.

Merci pour les liens et la remarque.

Sinon j'ai voulu essayer par composition mais ça ne marche pas vraiment puisque j'ai ça.

1/(z²+1)^s =f1of2of3(z) où :

f3(z) = z² holomorphe sur C entier
f2(z) = (1+z)^s, s complexe holomorphe sur D(0,1-) d'apres mon cours (mais d'ailleurs je n'arrive pas a comprendre pourquoi, et aussi pourquoi il n'y a pas des conditions sur s vu que d'apres l'énoncé Omega depend de s...)
f1(z)=1/z holomorphe sur C*.

En conclusion j'ai ma fonction par composition holomorphe sur D(0,1-) si je ne me suis pas trompé... Or on est loin de mon Omega. D'où cela vient ?

[Arkhnor]

On t'a défini la fonction (1+z)^s uniquement par son développement en série en 0 ?
Si oui, en effet, tu ne peux pas dire grand chose de plus.

L'énoncé suppose la détermination du logarithme connue, ce qui permet de définir les fonctions puissances bien au delà du domaine de convergence de la série.

[Azuriel]

Bah oui apparemment cette fonction est définie au delà du disque unité sinon je ne peux répondre a la question qui m'est posé. Mais je trouve donc ça bizarre que dans le cours il ne précise pas qu'en réalité elle est holomorphe au delà...

Mais alors comment montré que (1+z)^s est holomorphe au delà de D(0,1-) ?

Car j'ai l'impression que si je dis que (1+z)^s = (1-z0+(z-z0))^s qui est developpable en serie entiere si |z-z0|<|1-z0| alors je montre qu'elle est holomorphe sur C\{1}...

Le raisonnement est il juste ? ou sinon comment faire ?

[Arkhnor]

Comme je te l'ai dit, il faut définir (z+1)^s !! Comment définis-tu les puissances complexes autrement ?!
Il faut donc passer par le logarithme, et la formule (z+1)^s = exp(sLog(z+1)), comme pour le cas réel, et c'est comme cela que l'on montre que cette fonction est holomorphe. (cela suppose connu le logarithme complexe !)

Sinon, que dis exactement ton cours sur les puissances complexes ?

[Azuriel]

Là est le probleme c'est que je n'ai rien sur mon cours parlant des puissances complexes et c'est pour cela que je ne sais pas comment "gérer cette puissance de s". La seule chose que j'ai c'est dans l'énoncé l'inégalité sur le module de z^s.

Après j'ai retrouver une note sur un powerpoint trouvé sur le site du prof mais je n'ai pas plus de details. Cette note dit que :

z-> exp(z) est biholomorphe de {z, alpha<Im(z)<alpha + 2*Pi} sur C\R+*exp(i*alpha) (je comprend ça comme C privé de la demi droite qui fait un angle alpha avec R+).

Log alpha est donc la fonction inverse de exp.

Pour la determination principal du log on a alpha = - Pi donc c'est une fonction apparemment (bi ?)holomorphe de C\R- (comme tu me l'as dit).

Enfin on defini la fonction puissance comme tu me l'as dis :

si s complexe, z^s=exp(slogz); fonction multivaluée (je sais pas ce que ça veut dire par contre) si s n'est pas entier relatif.

Voila j'ai rien d'autre...

[Arkhnor]

Si tu n'as pas vu ça en cours, alors tu ne disposes pas du matériel suffisant pour résoudre l'exercice, mais tu verras forcément tout ça en cours.

Avec les notes que tu mentionnes, tu as tout ce qu'il faut. Est-ce que tu as besoin d'éclaircissements ?

Le terme fonction multivaluée est un terme un peu ambigüe qui signifie qu'en fait, on a plusieurs choix pour définir ces fonctions.
Par exemple, pour la racine carrée, on peut définir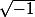 par i, ou par -i, et ce problème se répercute globalement sur la fonction réciproque que tu cherches à définir.

[Azuriel]

Alors il faut que j'utilise les notes.

Si je reconsidere (1+z)^s=exp(slog(1+z))

Alors log(1+z) est holomorphe sur C\R- -1.

Et exp est biholomorphe sur {z, 0<Im(z)<2*Pi} donc il faut que j'ai :

Im(s*log(1+z)) compris dans 0, 2Pi...ce qui est toujours le cas...non ?

Alors je sens que je ne suis plus tres loin de mon espace omega car j'ai le C\R- -1 qui ressemble un peu a mon [i, iinfini[ mais il faudrai donc multiplier par un i venant de s ou je ne sais pas quoi...

En fait je n'arrive pas a conclure maintenant...Comment faire ?

[Arkhnor]

Le caractère biholomorphique de l'exponentielle sur le domaine que tu mentionnes ne sert qu'à (entre autre) définir le logarithme.
L'exponentielle est définie sur C tout entier et y est holomorphe. (on dit qu'elle est entière) (le rayon de convergence de sa série en 0 est infini)
Donc l'exponentielle d'un nombre complexe est toujours défini.

Ce qu'il faut donc voir, c'est pour quels z log(z²+1) est défini, c'est à dire pour quel z, z²+1 est dans C\R-. (domaine de définition du log)

[Azuriel]

D'accord donc au final (1+z)^s est holomorphe sur C\R-.

Et donc en composant avec ce que j'avais dit il y a quelque message je trouve que 1/(1+z²)^s est holomorphe sur l'ensemble tel que pour tout z appartenant a cet ensemble on ai : "1+z² appartient a C\R-" ET "(1+z²) non nul" ce qui équivaut bien a mon espace Omega :).

Merci beaucoup pour ton aide et tes éclarcissements sur des points de cours !

[Arkhnor]

De rien ! :happy3:

N'hésite pas à reposer des questions, ce n'est pas forcément évident au premier abord.

[Azuriel]

Re !

Quelques question plus tard on reparle de ma fonction fs et on me demande de montrer que fs peut se prolonger en une fonction méromorphe (on me dit que qu'une fonction est méromorphe si elle est quotient de 2 fonctions holomorphes) sur le demi plan Im(z) > -1 si et seulement si s est entier relatif.

Alors je ne suis pas du tout sur du raisonnement qu'il faut adapter pour montrer cela... En effet je suis toujours un peu "frais" avec les series holomorphes et surtout j'ai peut etre une idée pour montrer l'inclusion dans un sens mais je ne suis meme pas sur que ce soit valable.


En effet, si s est entier relatif j'ai l'impression que la formule du binome de newton me donne tout de suite qu'en tout z, ma fonction (1+z²)^s est développable en serie entière et j'ai donc le quotient de la fonction holomorphe 1 et (1+z²)^s.

Mais cela me parait un peu bizarre... Quel est l'attitude a adpoter dans ce cas là ? Et comment montrer l'équivalence ?

Merci d'avance.

[kolmogorov]

bonjours,c'est komogorov avec toi
regarder bien j'ai bien lu ton message et j'ai resté une heure pour vous répondre
en théorie des fonctions d'une varieble complexe on doit étre prudent
la démonstration qu'une fonction soit analytique et de verifier les équations de chauchy-Riemann ,à ce moment la une condition necéssaire et suffisante.
maintenant on veut savoire l'analyticité de cette fonction donc on doit la représentée en serie de Laurent f(z)=som(a(n)z^n),n=-inf...inf
donc essayer de faire toutt cette démarche et repond moi.
pour finir le nombre s=a+ib .a,b appartien tà R

[Azuriel]

Oui ça j'avais compris, mais ici s est un entier donc pas besoin d'utiliser s=a+ib et puis on ne veut pas montrer que la fonction est analytique mais quotient de fonction analytique alors je comprends pas trop ce qu'il faut que je fasse par rapport à ton message...

[Arkhnor]

Re !

Il est clair que ce qui cause problème, c'est le prolongement sur la demi-droite (que je noterai d par la suite) qu'on a retiré au demi-plan pour construire l'ouvert Oméga.

L'implication inverse est aisée : si s est un entier relatif, l'expression est parfaitement définie (multiplication et division des complexes), sans avoir recours au logarithme.
Si s est positif, c'est donc le quotient de la fonction constante égale à 1 (évidemment holomorphe), et de la fonction elle aussi holomorphe sur le demi-plan (c'est un polynôme !).
On traite de manière similaire le cas s négatif.
De plus, cette fonction définie sur tout le demi-plan coïncide avec la fonction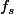 sur l'ouvert Oméga (le vérifier), c'est donc un prolongement méromorphe.

La réciproque est plus délicate. (quoique)
Suppose que l'on puisse prolonger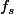 sur tout le demi-plan par une fonction de la forme 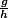, avec g et h holomorphes, et h non constante égale à 0.
h ne s'annule pas sur toute la demi-droite d (sinon elle serait nulle partout !)
Il existe donc un point de d où g/h est défini et est holomorphe, et en particulier continue. Ainsi, comme g/h prolonge 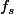(de manière continue), on en déduit que tend vers la même valeur lorsque tend vers par la droite et par la gauche (faire un croquis si ce n'est pas clair, on a plusieurs manières de s'approcher de , et en particulier, soit en restant dans quart de plan à droite, soit le quart de plan à gauche)

Or ces limites sont calculables, avec l'expression de sous forme .
Calcule ces deux limites (il faudra utiliser la définition du logarithme que j'ai introduite dans mon premier message), et vérifie qu'elles ne sont égales que si s est un entier relatif.

:happy3:

[Azuriel]

Arkhnor, tu dechires ^^.

Pour le sens s entier relatif => fonction meromorphe c'est en effet evident car on a soit l'inverse d'un polynome (si s est positif), soit un polynome directement si s<0 (c'est a dire notre fonction est donc même holomorphe).

De plus, cette fonction définie sur tout le demi-plan coïncide avec la fonction f_s sur l'ouvert Oméga (le vérifier)

Pour la vérification je ne sais pas comment la justifier tant ça me parait évident puisque nos polynomes sont égales a 1/(1+z²)^s et cela est vrai pour tout z dans C donc également pour Omega...

Est ce qu'il y a un moyen de mieux justifier en utilisant le thèoreme des zéro isolé pour montrer que fs-mon prolongement est identiquement nulle. Cependant il faudrait pour ça que je trouve une zone où il y a une "accumulation de zero" or je ne vois pas comment faire...


Pour la réciproque, j'avais en effet posé fs = g/h avec g et h holomorphe sur tout C mais je n'avais pas penser a quelque chose aussi simple que les limites pour dégager quelques choses sur s. Je vais tenter de calculer ça et je te tiens au courant mais de tout de façon j'ai encore ce petit probleme de justifier cleanement que mes fonctions coincide bien sur Omega (ça me parait un peu évident...).

EDIT : euh je dois vraiment merder quelque part mais je ne vois pas où car quand je calcule mes limites elles marchent toujours quelque soit s grrrr.

Voici mon raisonnement.

z0 appartient a d donc il s'écrit z0=a*exp(i*Pi/2) avec a réel superieur ou égale a 1.

Je vais donc approcher z0 par zgauche (noté zg) et zdroit (noté zd) tel que :

zg= a*exp(i*(Pi/2 + e)) et zd=a*exp(i*(Pi/2-e)) où e=epsilon que je fais tendre vers 0 pour faire tendre zg et zd vers z0.

J'utilise ensuite la formule du log(1+z²)=ln(|1+z²|)+iarg(1+z²)

où si z=x+iy on a arg(z)=2arctan(y/x+sqrt(x²+y²)).

En appliquant cette formule a zd et zg et en faisant la difference des deux termes et en faisant des DL, j'aboutis à :

limd-limg = lim Cste*2i*sin(2i*s*a²*2e/cste') qui est égale a 0...sans condition sur e.

Où est ce que je me suis gouré ?

Ou peut être faut-il que j'approche z0 différemment ?