Condition de diagonalisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Otsego
- Messages: 6
- Enregistré le: 24 Avr 2009, 14:24
-
 par Otsego » 24 Avr 2009, 14:39
par Otsego » 24 Avr 2009, 14:39
Bonjour,
Voici l'énoncé :
Dans R^3, A matrice associée à un endomorphisme f.
Dans la base canonique
A =
1 1 -1
1 1 1
1 1 1
1)Montrer que A est diagonalisable
2)calculer le polynome caracteristique de A.
Determiner les valeurs propres de A.
Quelle est la dimension des sous espaces propres?
Je ne voi pas comment repondre a la question 1 sans repondre a la question 2, y a il un moyen ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Avr 2009, 17:09
par Joker62 » 24 Avr 2009, 17:09
Tu es sûr de ta matrice ?
Elle serait pas symétrique par hasard ?
-
Otsego
- Messages: 6
- Enregistré le: 24 Avr 2009, 14:24
-
 par Otsego » 25 Avr 2009, 10:52
par Otsego » 25 Avr 2009, 10:52
oui je suis sur de la matrice, c'est tiré du sujet B de la banque PT 2008.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 26 Avr 2009, 09:14
par XENSECP » 26 Avr 2009, 09:14
En calculant A^2 et A^3 on trouve des trucs intéressants :)
Genre A^3-3A^2+2A = 0 ^^
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Avr 2009, 09:16
par Joker62 » 26 Avr 2009, 09:16
Oui mais le problème c'est que ça n'a rien d'un polynôme annulateur "simple"
Et en plus, c'est le polynôme caractéristique que tu donnes. Donc bon, y doit avoir un truc plus subtil :)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 26 Avr 2009, 09:23
par XENSECP » 26 Avr 2009, 09:23
Evidemment que c'est le PC... d'après Hamilton Cayley !
Enfin bon il est peut être pas simple mais avec un calculette, je l'ai trouvé en moins d'une minute :D
En même temps en regardant la matrice tu peux pas vraiment conclure... A part que 0 est vp simple et que la somme des 2 autres est 3 !
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Avr 2009, 09:38
par Joker62 » 26 Avr 2009, 09:38
Evidemment que c'est le polynôme Caractéristique ? J'vois pas ce qu'il y a d'évident là dedans mais bon...
Et donc, c'est ça le hic, on peut pas vraiment conclure. On est même pas censé savoir qu'il y a trois valeurs propres...
Bon 0 c'est sûr.
Le reste, mystère.
-
Otsego
- Messages: 6
- Enregistré le: 24 Avr 2009, 14:24
-
 par Otsego » 26 Avr 2009, 15:04
par Otsego » 26 Avr 2009, 15:04
donc le seul moyen de repondre a la question 1 reste de repondre a la question 2 ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Avr 2009, 15:21
par Joker62 » 26 Avr 2009, 15:21
Bé oui le sens habituel est de faire 2) puis de conclure par 1)
On connaît pas beaucoup de condition suffisante pour que A soit diagonalisable sans utiliser le polynôme caractéristique ni les valeurs propres...
On peut voir le sujet ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Avr 2009, 15:40
par Nightmare » 26 Avr 2009, 15:40
Salut :happy3:
Si on veut vraiment se passer du polynôme caractéristique ici, on peut simplement écrire la décomposition de Dunford de A :
}_{=D}+\(0\0\;2\\0\;0\;0\\0\;0\;0\))
D est trivialement diagonalisable (0 valeur propre double puisqu'elle est de rang 1 et 3 est une valeur propre simple).
A est donc diagonalisable.
On peut d'ailleurs répondre rapidement aux autres questions puisqu'alors
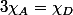
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Avr 2009, 16:01
par Joker62 » 26 Avr 2009, 16:01
C'est A-N qui est diagonalisable et qui a le même polynôme caractéristique que D non ?
(Avec N la matrice de la décomposition)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Avr 2009, 16:09
par Nightmare » 26 Avr 2009, 16:09
Non c'était bien A tout court mais de toute façon je viens de me rendre compte que mes deux matrices ne commutent pas donc ça marche pas :(
Edit : Non évidemment tu as raison, A est diagonalisable ssi la matrice nilpotente est nulle. Toute façon la question n'a pas lieu d'être vu que ce que j'ai donné n'est pas une décomposition de Dunford ! Je cherche une autre méthode.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 26 Avr 2009, 17:14
par Maxmau » 26 Avr 2009, 17:14
Nightmare a écrit:Salut :happy3:
Si on veut vraiment se passer du polynôme caractéristique ici, on peut simplement écrire la décomposition de Dunford de A :
}_{=D}+\(0\0\;2\\0\;0\;0\\0\;0\;0\))
D est trivialement diagonalisable (0 valeur propre double puisqu'elle est de rang 1 et 3 est une valeur propre simple).
A est donc diagonalisable.
On peut d'ailleurs répondre rapidement aux autres questions puisqu'alors
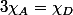
Bonjour
Es tu vraiment sûr de ton raisonnement ??
Id + N (N: nilpotente non nulle ) n'est pas diagonalisable
Je viens de voir ton correctif Ok

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 26 Avr 2009, 17:38
par leon1789 » 26 Avr 2009, 17:38
Heu, pour la première question, on peut faire semblant d'intuiter des choses ?
Oh, (1,-1,0) est dans le noyau !
Oh, (0,1,1) a pour image 2 fois lui-même !
Oh, (-1,1,1) est fixé par la matrice !
Non ?
EDIT : bon, ok, ça fait tourner l'exo à l'envers... pas terrible.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Avr 2009, 17:51
par Joker62 » 26 Avr 2009, 17:51
-
Otsego
- Messages: 6
- Enregistré le: 24 Avr 2009, 14:24
-
 par Otsego » 27 Avr 2009, 09:22
par Otsego » 27 Avr 2009, 09:22
bien joué pour la trouvaille, merci!
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 27 Avr 2009, 10:22
par Joker62 » 27 Avr 2009, 10:22
Oui bon si c'est un DM pour les vacances, fais semblant d'avoir bosser quand même lol
-
Otsego
- Messages: 6
- Enregistré le: 24 Avr 2009, 14:24
-
 par Otsego » 27 Avr 2009, 13:21
par Otsego » 27 Avr 2009, 13:21
non c'est pas du tout un DM, je passe la banque pt dans une semaine!
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 27 Avr 2009, 13:33
par Joker62 » 27 Avr 2009, 13:33
Ah oki

Bé y'a tout les sujets ici alors [url="http://pagesperso-orange.fr/cristofari/devoirs.htm"]http://pagesperso-orange.fr/cristofari/devoirs.htm[/url]
Bon courage

-
Otsego
- Messages: 6
- Enregistré le: 24 Avr 2009, 14:24
-
 par Otsego » 27 Avr 2009, 16:44
par Otsego » 27 Avr 2009, 16:44
Oui j'ai fait un peu le tour encore merci.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
