Analyse Complexe

[marie49]

Bonjour à tous!

En analyse complexe il y a une démonstration que je ne comprend pas...
Il s'agit de démontrer que :

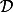
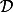
Si est le disque unité ouvert et , l'homographie définie par : est une bijection holomorphe de sur lui-même, d'inverse

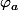
Au début de la démonstration, le prof a écrit : comme , est holomorphe sur .

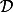
D'où vient ce résultat? (c'est la rentrée, pas facile de se remettre dans les cours, je suis un peu larguée! :hein: )

Merci d'avance pour votre aide!

[Nightmare]

Salut :happy3:

Eh bien est le seul pôle de ton homographie et il n'est pas dans le disque unité donc cette dernière est holomorphe sur D tout entier

[marie49]

Ok merci!
Vraiment dure la rentrée! :ptdr:
Faut que je reprenne le rythme!

Désolée d'avoir ouvert un post pour un truc aussi évident. :stupid_in
Merci

[mathelot]

re,

finalement, j'ai trouvé cette feuille d'exos:

içi

Grâce au lemme de Schwarz, on détermine tous les automorphismes
analytiques du disque unité.

Question: y a t il un lien avec la géométrie hyperbolique ?

merçi d'avance.