Petit calcul
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 03 Sep 2008, 15:25
par nivéa » 03 Sep 2008, 15:25
Cauchy3 a écrit:Ah, tout est bon sauf que vous avez oublié un carré pour x et y lorsque vous avez écrit les premières dérivées partielles.
On continue :
Vous êtes d'accord avec moi que la différence des deux équations nous donne y=x ou y=-x ce qui veut dire qu'il y ait deux cas à envisager, le cas y=x et le cas y=-x :
Question : Que devient le système lorsque y=x (c'est bien la question qu'il est impératif de poser lorsqu'on distingue des cas)?
je pense que je suis en panne d'énergie, je trouve un résultat qui n'a pas l'air très très juste!!! :girl2:
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 03 Sep 2008, 15:27
par Cauchy3 » 03 Sep 2008, 15:27
nivéa a écrit:je pense que je suis en panne d'énergie, je trouve un résultat qui n'a pas l'air très très juste!!! :girl2:
Vous avez beaucoup d'énergie et de capacité, montrez moi ce que vous avez trouvé, on discutera par la suite.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 03 Sep 2008, 15:33
par nivéa » 03 Sep 2008, 15:33
ce que je pense
je remplace x par y dans :
+1=0)
je trouve :

la racine doit aller sur tte la fraction.
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 03 Sep 2008, 15:44
par Cauchy3 » 03 Sep 2008, 15:44
nivéa a écrit:ce que je pense
je remplace x par y dans :
+1=0)
je trouve :

la racine doit aller sur tte la fraction.
J'ai bien dit : Que devient
LE SYSTÈME ?
Je réponds pour le cas y=x et je vous laisse faire l'autre cas.
Le système devient dans le cas y=x :
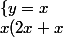+1=0)
Soit

La deuxième équation est impossible le système ne possède pas de solution.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 03 Sep 2008, 22:33
par nivéa » 03 Sep 2008, 22:33
Cauchy3 a écrit:J'ai bien dit : Que devient
LE SYSTÈME ?
Je réponds pour le cas y=x et je vous laisse faire l'autre cas.
Le système devient dans le cas y=x :
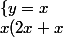+1=0)
Soit

La deuxième équation est impossible le système ne possède pas de solution.
si je fais maintenant y=-x
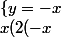+x)+1=0)
Soit-


-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 03 Sep 2008, 22:35
par Cauchy3 » 03 Sep 2008, 22:35
nivéa a écrit:si je fais maintenant y=-x
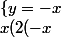+x)+1=0)
Soit-


Oui c'est bien ça, vous avez alors trouvé les points (-1;1) et (1;-1).
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 03 Sep 2008, 22:41
par nivéa » 03 Sep 2008, 22:41
je vais vous paraitre :marteau: mais la réponse (-1;1) et (1;-1). vient du fait que

et comme nous avons trouvé

, donc c'est pour ça qu'on trouve ces solutions nan!!
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 03 Sep 2008, 22:46
par nivéa » 03 Sep 2008, 22:46
Cauchy3 a écrit:J'ai bien dit : Que devient
LE SYSTÈME ?
Je réponds pour le cas y=x et je vous laisse faire l'autre cas.
Le système devient dans le cas y=x :
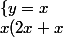+1=0)
Soit

La deuxième équation est impossible le système ne possède pas de solution.
je n'arrive aps à comprendre comment vous en déduisez qu'il n'y a pas de solution, ici

-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 03 Sep 2008, 22:49
par Cauchy3 » 03 Sep 2008, 22:49
nivéa a écrit:je n'arrive aps à comprendre comment vous en déduisez qu'il n'y a pas de solution, ici

L'équation 3x²+1=0 est équivalente à 3x²=-1, un nombre positif (3x²) ne peut pas être égal à un nombre négatif (-1).
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 03 Sep 2008, 22:54
par nivéa » 03 Sep 2008, 22:54
Cauchy3 a écrit:L'équation 3x²+1=0 est équivalente à 3x²=-1, un nombre positif (3x²) ne peut pas être égal à un nombre négatif (-1).
donc, si je comprend bien, si je me situe dans les cas y=-x, on trouve comme solution -
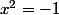
, alors ici on trouve deux nombres négatifs alors il y a solution!!
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 03 Sep 2008, 23:02
par Cauchy3 » 03 Sep 2008, 23:02
nivéa a écrit:donc, si je comprend bien, si je me situe dans les cas y=-x, on trouve comme solution

, alors ici on trouve deux nombres négatifs alors il y a solution!!
(sur le forum il y a un beug lorsque vous écrivez [TEX*]suivi d'un signe moins, pour cela il faut laissez un peu d'espace comme ceci
[TEX*] -x^2=-1[/TEX*] (évidemment sans les étoiles (asterix) je veux juste vous montrer).
Oui car -x²=-1 est équivalente à x²=1 ce qui signifie x²-1=0 donc (x-1)(x+1)=0 d'où les solutions, vous pouvez aussi la voire en écrivant

-
Argentoratum
- Membre Relatif
- Messages: 231
- Enregistré le: 12 Sep 2007, 22:35
-
 par Argentoratum » 03 Sep 2008, 23:04
par Argentoratum » 03 Sep 2008, 23:04
nivéa a écrit: ici

Si

, alors

et non pas

attention aux signes.
De plus le discriminant est négatif donc pas de solutions dans R.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 03 Sep 2008, 23:41
par nivéa » 03 Sep 2008, 23:41
Argentoratum a écrit:Si

, alors

et non pas

attention aux signes.
De plus le discriminant est négatif donc pas de solutions dans R.
Merci, je trouve bien un discriminant négatif, pas de sol ds IR.
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 04 Sep 2008, 20:19
par Cauchy3 » 04 Sep 2008, 20:19
Libérez votre boite de réception pour qu'on puisse vous envoyer un message privé.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 04 Sep 2008, 22:10
par nivéa » 04 Sep 2008, 22:10
je n'arrive pas à comprendre quelque chose: la différence entre le théorème des extremas liés et le multiplicateur de Lagrange.
Je n'explique dans un exercice, il me demande de déduire à l'aide de la méthode de Lagrange que la fonction étudiée présente 8 extremas dasn D1
=x^2+y^2+x^3y^3)
soit
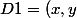:x^2+y^2=1\right)
.
Et dans cette exemple: soit
=2xy-x-y)
,il me demande d'appliquer le multiplicateur de lagrange pour trouver la valeur max et la valeur mini de la fonction f sur la courbe
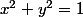
ma démonstration vous la retrouverez dans le topic:petit problème page2.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 11:11
par nivéa » 05 Sep 2008, 11:11
qui aurai une idée
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 11:25
par Cauchy3 » 05 Sep 2008, 11:25
nivéa a écrit:je n'arrive pas à comprendre quelque chose: la différence entre le théorème des extremas liés et le multiplicateur de Lagrange.
Je n'explique dans un exercice, il me demande de déduire à l'aide de la méthode de Lagrange que la fonction étudiée présente 8 extremas dasn D1
=x^2+y^2+x^3y^3)
soit
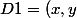:x^2+y^2=1\right)
.
Et dans cette exemple: soit
=2xy-x-y)
,il me demande d'appliquer le multiplicateur de lagrange pour trouver la valeur max et la valeur mini de la fonction f sur la courbe
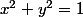
ma démonstration vous la retrouverez dans le topic:petit problème page2.
En fait il y a plusieurs méthodes pour optimiser une fonction avec une contrainte, il y a l'application du théorème de Lagrange (multiplicateur de Lagrange) il y a aussi celle de changement de variable.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 11:41
par nivéa » 05 Sep 2008, 11:41
Cauchy3 a écrit:En fait il y a plusieurs méthodes pour optimiser une fonction avec une contrainte, il y a l'application du théorème de Lagrange (multiplicateur de Lagrange) il y a aussi celle de changement de variable.
comment savoir, laquelle appliquer ?
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 12:21
par Cauchy3 » 05 Sep 2008, 12:21
Si par exemple la contrainte est sous la forme x²+y²=5 alors ici on préfère utiliser les coordonnées polaires
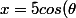 et y=5 sin(\theta))
afin de rendre le problème d'optimisation à une seule variable.
En générale lorsque cette méthode tombe en défaut on utilise la méthode de multiplicateurs de Lagrange (en fait il y en a d'autre méthodes).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
