Salut,
J'aurais quelque questions à vous poser :
- Quand peut-on dire d'une inégalité qu'elle est symétrique (pour pouvoir poser a>=b>=c par exemple) ?
- Quand peut-on dire d'une inégalité qu'elle est homogène (pour pouvoir poser a+b+c=1, abc=1, etc...)
Désolé de vous importuner par mes questions :ptdr:
A propos des inégalités
10 messages
- Page 1 sur 1
Salut 
Une inégalité symétrique permet en effet de pouvoir poser certaines conditions telles qu'un ordre entre les données.
Tu peux remarquer une symétrie (pas nécessairement dans une inégalité), lorsque les données peuvent être permutées sans modifier la structure.
Quelques exemples :


etc ...
Après pour l'homogénéité, je ne l'utilise pas donc je ne peux pas te dire, désolé.
Une inégalité symétrique permet en effet de pouvoir poser certaines conditions telles qu'un ordre entre les données.
Tu peux remarquer une symétrie (pas nécessairement dans une inégalité), lorsque les données peuvent être permutées sans modifier la structure.
Quelques exemples :
etc ...
Après pour l'homogénéité, je ne l'utilise pas donc je ne peux pas te dire, désolé.
On dit qu'une fonction  est homogène de degré
est homogène de degré  s'il existe un réel
s'il existe un réel  tel que pour tout réel
tel que pour tout réel  :
:
 = \lambda^{\alpha}f(a_1, a_2,\cdots, a_n))
En pratique, tu remplaces chacune de tes variables par et tu regardes s'il existe un réel
et tu regardes s'il existe un réel  (généralement, un entier naturel) tel que tu peux simplifier l'inégalité par
(généralement, un entier naturel) tel que tu peux simplifier l'inégalité par pour revenir à l'inégalité originelle. Dans ce cas, l'inégalité est dite homogène de degré
pour revenir à l'inégalité originelle. Dans ce cas, l'inégalité est dite homogène de degré  et tu peux supposer des contrainte du genre
et tu peux supposer des contrainte du genre 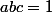 ,
, 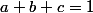 etc ... si elles n'existent pas déjà dans l'énoncé.
etc ... si elles n'existent pas déjà dans l'énoncé.
En pratique, tu remplaces chacune de tes variables par
Tu seras sûrement ammené aussi à rencontre le terme "somme cyclique" : une somme cyclique est invariante par permutation cyclique des variables, alors qu'une somme symétrique est invariante par permutation quelconque des variables.
(Si tu ne sais pas ce qu'est une permutation cyclique, voici un exemple. Les permutations cycliques de ABCDE sont : ABCDE, EABCD, DEABC, CDEAB, BCDEA. J'espère que l'exemple est clair.)
Exemples :
* x/y + y/z + z/x est une somme cyclique, parce que si, par exemple, on met y a la place de x, z a la place de y et x à la place de z (permutation cyclique des trois variables), on obtient y/z + z/x + x/y, i. e. la même somme. Par contre, ce n'est pas une somme symétrique, parce que si on permute y et z sans toucher à x, on obtient x/z + z/y + y/x, ce qui n'est pas la meme chose.
* x^2yz + xy^2z + xyz^2 est une somme symetrique.
Intuitivement, dans une somme cyclique, aucune variable ne joue un role different des autres, mais il y a tout de meme un ordre dans lequel les varialbes se suivent. En revanche, dans une somme symetrique, toutes les variables sont completement interchangeables.
On peut aussi parler de somme cyclique (ou symetrique) d'un membre. Cela signifie la somme de tous les membres obtenus par des permutations cycliques (ou symetriques) du membre en question. Par exemple (si on sait qu'il y a trois variables) :
 x/y = x/y + y/z + z/x
x/y = x/y + y/z + z/x
 x^2y = x^2y + xy^2 + x^2z + xz^2 + y^2z + yz^2.
x^2y = x^2y + xy^2 + x^2z + xz^2 + y^2z + yz^2.
Cette notation n'est pas rigoureuse (on ne la rencontrera jamais dans un enonce), mais elle a l'avantage de raccorcir l'ecriture et de la rendre plus claire.
Attention : quand on ecrit somme symetrique de xyz (avec trois variables), le resultat n'est pas xyz, mais 6xyz. En effet, il y a 6 permutations de trois variables, donc 6 membres - meme si en l'occurrence, ils sont tous egaux.
(Si tu ne sais pas ce qu'est une permutation cyclique, voici un exemple. Les permutations cycliques de ABCDE sont : ABCDE, EABCD, DEABC, CDEAB, BCDEA. J'espère que l'exemple est clair.)
Exemples :
* x/y + y/z + z/x est une somme cyclique, parce que si, par exemple, on met y a la place de x, z a la place de y et x à la place de z (permutation cyclique des trois variables), on obtient y/z + z/x + x/y, i. e. la même somme. Par contre, ce n'est pas une somme symétrique, parce que si on permute y et z sans toucher à x, on obtient x/z + z/y + y/x, ce qui n'est pas la meme chose.
* x^2yz + xy^2z + xyz^2 est une somme symetrique.
Intuitivement, dans une somme cyclique, aucune variable ne joue un role different des autres, mais il y a tout de meme un ordre dans lequel les varialbes se suivent. En revanche, dans une somme symetrique, toutes les variables sont completement interchangeables.
On peut aussi parler de somme cyclique (ou symetrique) d'un membre. Cela signifie la somme de tous les membres obtenus par des permutations cycliques (ou symetriques) du membre en question. Par exemple (si on sait qu'il y a trois variables) :
Cette notation n'est pas rigoureuse (on ne la rencontrera jamais dans un enonce), mais elle a l'avantage de raccorcir l'ecriture et de la rendre plus claire.
Attention : quand on ecrit somme symetrique de xyz (avec trois variables), le resultat n'est pas xyz, mais 6xyz. En effet, il y a 6 permutations de trois variables, donc 6 membres - meme si en l'occurrence, ils sont tous egaux.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
