Pour les grands maîtres des inégalités [Résolu]
Olympiades mathématiques, énigmes et défis
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 25 Déc 2010, 23:10
par girdav » 25 Déc 2010, 23:10
Bonjour,
on se donne un entier

et
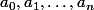
des nombres réels positifs tels que pour tout
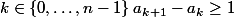
. Montrer que
[CENTER]
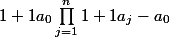\leq \prod_{j=0}^n\(1+\fr 1{a_j}\).)
[/CENTER]
Quels sont les cas d'égalité?

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 25 Déc 2010, 23:44
par Olympus » 25 Déc 2010, 23:44
Salut !
Sauf erreur, l'inégalité est fausse pour
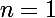
car
 = \frac{-\left(a_0-a_1\right)^2 - a_1 }{a_0 a_1 \left(a_1 - a_0 \right)} \leq 0)
.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 25 Déc 2010, 23:49
par girdav » 25 Déc 2010, 23:49
Olympus a écrit:Salut !
Sauf erreur, l'inégalité est fausse pour
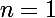
car
 = \frac{-\left(a_0-a_1\right)^2 - a_1 }{a_0 a_1 \left(a_1 - a_0 \right)} \leq 0)
.
Salut,
oui évidemment si j'oublie un facteur en cours de route... J'ai corrigé.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 26 Déc 2010, 14:21
par Olympus » 26 Déc 2010, 14:21
Franchement, je sèche totalement là :marteau:
Je l'ai démontrée pour n=1 . Ce qui nous donne
\right)-\frac{n}{a_{n+1}})
au cas où on veut procéder par récurrence, sauf que je ne vois pas comment m'en servir ...
J'ai aussi remarqué que
)
, mais c'est pas assez fort pour conclure

Une indice ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2010, 14:29
par girdav » 26 Déc 2010, 14:29
On peut montrer l'inégalité par récurrence. C'est bien sûr l'héridité qui va nous occuper (l'initialisation est presque triviale une fois que l'énoncé est correct).
Supposons la propriété vraie au rang

. Il "suffit" de montrer que
[CENTER]
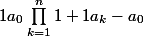\fr 1{a_{n+1}-a_0}\leq \prod_{k=0}^n\(1+\fr 1{a_k}\)\fr 1{a_{n+1}}.)
[/CENTER]

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 26 Déc 2010, 15:18
par Olympus » 26 Déc 2010, 15:18
Lol, tu m'as presque donné la solution là, c'est évident maintenant xD
Cela vient du fait que
 \right) - \frac{1}{a_0 \left(a_{n+1}-a_0\right)} \bigprod_{k=1}^n \left(1+\frac{1}{a_k-a_0}\right) = \frac{1}{a_{n+1}} \left( 1 - \frac{1}{a_{n+1}-a_0} \bigprod_{k=1}^n \left(1+\frac{1}{a_k - a_0 \right) \right))
Mais vu que

, on a immédiatement
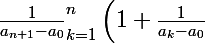 \leq \frac{1}{n+1} \bigprod_{k=1}^n \left(1+\frac{1}{k} \right) = \frac{1}{n+1} \times \frac{ \left(n+1\right)!}{n!}=1)
.
D'où le résultat .
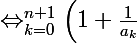 \geq \bigprod_{k=0}^n \left(1+\frac{1}{a_k} \right) + \frac{1}{a_0} \bigprod_{k=1}^n \left(1+\frac{1}{a_k-a_0} \right) \frac{1}{a_{n+1}-a_0})
On utilise l'hypothèse de récurrence encore une fois et c'est fini car :
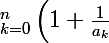 + \frac{1}{a_0} \bigprod_{k=1}^n \left(1+\frac{1}{a_k-a_0} \right) \frac{1}{a_{n+1}-a_0} \geq 1+ \frac{1}{a_0} \bigprod_{k=1}^n \left(1+\frac{1}{a_k-a_0}\right) + \frac{1}{a_0}\bigprod_{k=1}^n \left(1+\frac{1}{a_k-a_0} \right)\frac{1}{a_{n+1}-a_0} = 1+ \frac{1}{a_0} \bigprod_{k=1}^{n+1}\left(1+\frac{1}{a_k-a_0}\right))
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2010, 15:26
par girdav » 26 Déc 2010, 15:26
Olympus a écrit:Lol, tu m'as presque donné la solution là, c'est évident maintenant xD
Disons que c'était tout ou rien. Si je disais "essaie de montrer une inégalité intermédiaire", tu n'aurais peut-être pas été beaucoup plus avancé.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 26 Déc 2010, 15:38
par Olympus » 26 Déc 2010, 15:38
girdav a écrit:Disons que c'était tout ou rien. Si je disais "essaie de montrer une inégalité intermédiaire", tu n'aurais peut-être pas été beaucoup plus avancé.
Oui, je passais du temps à essayer diverses applications de Cauchy-Schwarz et Tchebyshev sans aboutir à quelque chose et j'aurais continué si tu ne m'avais pas donné ton indice :ptdr: Alors que là, je suis étonné par la simplicité de la solution :doh:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2010, 15:41
par girdav » 26 Déc 2010, 15:41
Maintenant il ne reste plus que les cas d'égalité mais effectivement le plus dur est derrière.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 26 Déc 2010, 16:28
par Olympus » 26 Déc 2010, 16:28
On montre aisément par récurrence qu'il y a égalité si et seulement si

.
Pour n=1, c'est évident .
On suppose que pour un certain 'n',
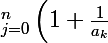 = 1+\frac{1}{a_0} \bigprod_{j=1}^n \left( 1+\frac{1}{a_j - a_0} \right) \Leftrightarrow \forall k \in \left\{ 0;1;...;n-1 \right\} \qquad : \qquad a_{k+1}-a_k=1)
.
On résout
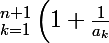 = 1 + \frac{1}{a_0} \left(1+\frac{1}{a_{n+1}-a_0} \right)\bigprod_{k=1}^{n} \left(1+\frac{1}{a_k-a_0} \right))
 - 1 - \frac{1}{a_0} \bigprod_{k=1}^n \left(1+\frac{1}{a_k-a_0}\right) \right) + \left( \frac{1}{a_{n+1}} \bigprod_{k=0}^n\left(1+\frac{1}{a_k} \right) - \frac{1}{a_0 \left( a_{n+1} - a_0 \right) } \bigprod_{k=1}^n \left(1+\frac{1}{a_k-a_0} \right) \right) = 0)
 &=& 0 \\<br />\end{array} \right.)
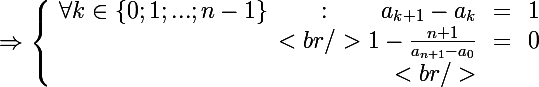
Or
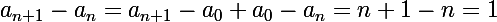
.

Réciproquement, on a bien une égalité sous cette dernière condition si on remplace dans la troisième ligne .
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2010, 16:48
par girdav » 26 Déc 2010, 16:48
Je suis d'accord. En fait ici au vu de l'hypothèse on se doute des cas d'égalité.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités