Aire ...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 25 Avr 2008, 21:49
par itouchu » 25 Avr 2008, 21:49
Ok ok merci :)

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 25 Avr 2008, 21:57
par Sa Majesté » 25 Avr 2008, 21:57
Ouaip sauf que tu as calculé V2 et pas U2 ! :happy2:
Pour les Un il faut prendre les rectangles intérieurs (ils ne dépassent pas la courbe)
Pour les Vn il faut prendre les rectangles extérieurs (ils dépassent pas la courbe)
La suite Un minore l'intégrale de 0 à 1 de f(x)dx
La suite Vn majore l'intégrale de 0 à 1 de f(x)dx
Les 2 suites sont adjacentes et ont pour limite cette intégrale
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 25 Avr 2008, 22:06
par itouchu » 25 Avr 2008, 22:06
Ok Merci bcp !
Je revois sa demain...
Bonne soirée !
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 26 Avr 2008, 10:17
par itouchu » 26 Avr 2008, 10:17
Après pour montrer les expressions de Un et Vn, je peux commencer par quoi ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Avr 2008, 10:26
par Sa Majesté » 26 Avr 2008, 10:26
Il faut utiliser l'aire du rectangle k^3 / n^4
Bien sûr il faut sommer pour k entre 0 et n-1 pour avoir Un
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 26 Avr 2008, 10:35
par itouchu » 26 Avr 2008, 10:35
Sommer cest a dire que je dois calculer l'intégrale de k^3 / n^4 pour k la somme de 0 à n-1 ?
Je trouve (n-1)^4/4n^4

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Avr 2008, 10:43
par Sa Majesté » 26 Avr 2008, 10:43
Non c'est une somme finie, pas une intégrale
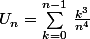
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 26 Avr 2008, 10:48
par itouchu » 26 Avr 2008, 10:48
Ok j'utilise la formule pour la somme :
S = (n+1)(Uo+Un)/2
Un = (n+1)(0+(n-1))/2
Un = (n-1)²/2 ... :briques:

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Avr 2008, 10:55
par Sa Majesté » 26 Avr 2008, 10:55
Non
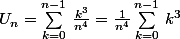
Après il faut savoir que :
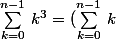^2)
Cette formule se démontre par récurrence
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 26 Avr 2008, 11:08
par itouchu » 26 Avr 2008, 11:08
Oui c'est ok ...
Et j'imagine que c'est idem pour Vn !
:we:
Pour montrer que (Un) et (Uv) adjacentes :
Je les dérive ou il ya un moyen plus simple ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Avr 2008, 11:15
par Sa Majesté » 26 Avr 2008, 11:15
itouchu a écrit:Pour montrer que (Un) et (Uv) adjacentes :
Je les dérive ou il ya un moyen plus simple ?
Dériver des suites ? :marteau: :mur:
Une suite est une fonction définie sur IN (ou une partie de IN)
Or IN est un ensemble discret, il ne contient aucun intervalle ouvert donc par nature une suite ne peut pas être continue et encore moins dérivable
Pour trouver le sens de variation d'une suite, plusieurs méthodes :
1) étude du signe de
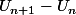
2) étude de
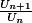
3) si la suite est définie de façon explicite (Un=f(n)) alors on peut étudier les variations de f sur IR (et là on peut dériver)
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 26 Avr 2008, 12:14
par itouchu » 26 Avr 2008, 12:14
1) étude du signe de U_{n+1} - U_n
Pour Un je trouve :
-2n²+n+2 / 2n²+2
Je suis pas sur, je pense que je me suis planté dans le developpement ...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Avr 2008, 18:13
par Sa Majesté » 26 Avr 2008, 18:13
itouchu a écrit:1) étude du signe de U_{n+1} - U_n
Il faut aussi copier-coller les balises LATEX ! :ptdr:
itouchu a écrit:Pour Un je trouve :
-2n²+n+2 / 2n²+2
Je suis pas sur, je pense que je me suis planté dans le developpement ...
Exact tu t'es planté !
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 26 Avr 2008, 19:59
par itouchu » 26 Avr 2008, 19:59
Oui mais bon c'est quand même des calculs compliqués ?
Pour exprime le Un+1 = [((n+1)-1)/2(n+1)]² ?
Donc
Un+1 - Un = [((n+1)-1)/2(n+1)]² - [(n-1)/2n]²
Pour savoir déjà si je démarre bien ...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Avr 2008, 20:01
par Sa Majesté » 26 Avr 2008, 20:01
Tu démarres bien :zen:
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 26 Avr 2008, 20:25
par itouchu » 26 Avr 2008, 20:25
Sa fait 3 fois que je recommence les calculs, je trouve différent à chaque fois !
Tu ne pourrais pas me donner ton résultat final ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Avr 2008, 20:33
par Sa Majesté » 26 Avr 2008, 20:33
itouchu a écrit:Sa fait 3 fois que je recommence les calculs, je trouve différent à chaque fois !
Tu ne pourrais pas me donner ton résultat final ?
Je pourrais mais c'est contraire au règlement du forum que tout-un-chacun doit s'efforcer de suivre le plus scrupuleusement possible :jap: :langue:
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 26 Avr 2008, 21:15
par itouchu » 26 Avr 2008, 21:15
Okay bon je passe cette question ...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 27 Avr 2008, 10:19
par Sa Majesté » 27 Avr 2008, 10:19
D'après les questions précédentes
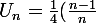^2)
La limite de Un n'est pas trop difficile à trouver
-
itouchu
- Membre Naturel
- Messages: 50
- Enregistré le: 29 Fév 2008, 18:23
-
 par itouchu » 27 Avr 2008, 10:46
par itouchu » 27 Avr 2008, 10:46
Dacord, c'est bon j'ai trouvé 1/4 en mettant les n en facteurs ... on obtient 1/4 comme limite :++:
Je voulais revenir au problème des Un+1 - Un
On avait bien [((n+1)-1)/2(n+1)]² - [(n-1)/2n]²
On reconnait l'identité remarquable a² - b² , on doit l'utilisé ? ou c'est mieux de développer avec le carré les expressions ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
