Equation differentielle

par **georgess** » 05 Fév 2008, 22:37

je suis très faible en formule de trigo , je sais que sin²x + cos²x = 1 mais ma formule de départ c'est (-sin x - cos²x) / sin²x , donc je vois pas de rapport...

par **Elvix** » 05 Fév 2008, 22:40

Allez, un tout petit effort: -cos²-sin² = -(...) = ...
Accélère qu'on puisse passer à l'exo suivant :dodo:

par **nuage** » 05 Fév 2008, 22:43

La dérivée de

est

d'après ton calcul (et le mien). Donc les primitives de

sont de la forme

C constante.
De plus

.
En fait une fois que l'on a trouvé la solution particulière

facile à vérifier, l'exercice est terminé.

A+

par **georgess** » 05 Fév 2008, 22:45

non je suis désolé je vois pas le rapport avec la formule que j'ai donné je te l'ai dit je suis 0 / 20 en changement de formule de trigo ça me plombe tous mes exos ...

quelle rapport entre - (cos²x + sin²x) et (-sin x - cos²x) / sin²x

par **Elvix** » 05 Fév 2008, 22:46

il n'y a pas de formule trigo:
(-sin²x-cos²x)/sin²x=-1/sin²x, c'est tout

par **georgess** » 05 Fév 2008, 22:47

attendez je me suis planté dans ma dérivée de départ pour ça quer je devenais fou , laissez moi 5 min svp pour me corriger

par **nuage** » 05 Fév 2008, 22:50

par **georgess** » 05 Fév 2008, 22:56

ben oui j'avais oublié un exposant carré , maintenant tout est clair , c'est dingue le temps qu'on peut perdre pour ces sotises , à la rigueur !!!!!!!!!!!

dernière question de l'exercice :

calculer la solution avec les conditions initiales y(pi/2) = 1 . que se passe t'il en 0 et en pi ? pouvait on le prévoir ?

-cos(pi/2) + C sin(pi/2) = 1

C = 1

Alors en 0 il se passe que ya pas de solutions et en pi C peut prendre pleins de valeurs différentes , toutes sur R !

vous etes d'accord ?

par **nuage** » 05 Fév 2008, 23:02

Non.
En 0 on a un point critique car sin 0 =0 et l'équation devient
-y(0) cos 0 =1 d'où y(0) = -1.
Si je me souviens bien de l'équation de départ.

[modification]
Mes excuses pour une lecture trop rapide.
Oui, toutes les valeurs de C conviennent et donnent

par **georgess** » 05 Fév 2008, 23:10

pas grave , merci à vous 2 pour votre aide préciseuse et désolé mais je débute en equa diff et l'exercice que j'ai fait c'est pas le mieux conseillé pour débuter , merci bcp .

par **nuage** » 05 Fév 2008, 23:14

Une dernière remarque : on a un problème de raccordement dès que

.
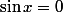
En d'autres termes on a un problème si

si tu débute c'est un peu délicat.

Equation differentielle

Qui est en ligne