Le Grand Theoreme De Fermat
16 messages
- Page 1 sur 1
Le Grand Theoreme De Fermat
BONSOIR
VOILA QUE DEPUIS UNE TRENTAINE DE JOURS JE ME SUIS PENCHE SUR LE PROBLEME DE FERMAT....VOILA CE QUE J'AI REUSSI A DEMONTRER:
Si X^n+Y^n=Z^n avec n premier >2 et XYZ non nul et X, Y,Z premiers deux a deux et X et Y premier avec n ALORS:
SI Z est premier avec n alors:
X+Y est une puissance n eme
Z-Y est une puissance n eme
Z- X est une puissance n eme
ET DONC Z congru a X+Y modulo n²
ET AUSSI X^(n-1) , Y^(n-1) ,Z^(n-1) sont congrus a 1 modulo a n² (trés ressemblant a Wieferich!)
Si n divise Z:
n(X+Y) est une puissance n eme
Z-Y est une puissance n eme
Z- X est une puissance n eme
qu'en pensez vous?cela at-il deja été demontré?
je voudrais rajouter que cette methode ma permis de retrouver les triplets pythagoriciens primitifs......Et en plus de voir ou eté le probleme lorsque n depassé 2.....
ON remarquera que le premier cas ecarte immediattement 2....car imp+imp n'est pas impair!
De plus les hypotheses font perdre la generalité de l'equation lorsque n=2 et pas pour n>2 car alors n est impair et les hypotheses ne font perdre aucune generalité.
Cordialement
VOILA QUE DEPUIS UNE TRENTAINE DE JOURS JE ME SUIS PENCHE SUR LE PROBLEME DE FERMAT....VOILA CE QUE J'AI REUSSI A DEMONTRER:
Si X^n+Y^n=Z^n avec n premier >2 et XYZ non nul et X, Y,Z premiers deux a deux et X et Y premier avec n ALORS:
SI Z est premier avec n alors:
X+Y est une puissance n eme
Z-Y est une puissance n eme
Z- X est une puissance n eme
ET DONC Z congru a X+Y modulo n²
ET AUSSI X^(n-1) , Y^(n-1) ,Z^(n-1) sont congrus a 1 modulo a n² (trés ressemblant a Wieferich!)
Si n divise Z:
n(X+Y) est une puissance n eme
Z-Y est une puissance n eme
Z- X est une puissance n eme
qu'en pensez vous?cela at-il deja été demontré?
je voudrais rajouter que cette methode ma permis de retrouver les triplets pythagoriciens primitifs......Et en plus de voir ou eté le probleme lorsque n depassé 2.....
ON remarquera que le premier cas ecarte immediattement 2....car imp+imp n'est pas impair!
De plus les hypotheses font perdre la generalité de l'equation lorsque n=2 et pas pour n>2 car alors n est impair et les hypotheses ne font perdre aucune generalité.
Cordialement
Le grand théoreme de fermat a déjà ete demontré...en 1996
http://www.bibmath.net/dico/index.php3?action=affiche&quoi=./f/fermatgd.html
...
http://www.bibmath.net/dico/index.php3?action=affiche&quoi=./f/fermatgd.html
...
CERTEs
Salut Cesar
Comme tu l'as dis Le theoreme de Fermat Wiles a deja eté demontré....mais la n'est pas la question, la question qui reste tout de meme , en tout cas pour moi d'actualité est "existe t-il une demonstration "elementaire" du theoreme de fermat" ?
Ayant obtenue ces droles d'equations je me suis dis que j'allais les presenter sur un forum afin de voir si cela a deja été demontré , et sinon quelqu'un a t-il une idée pour continuer et trouver une absurdité
Bien evidemment j'ai tenté de montrer que X-Y etait une puissance n'eme afin d'utiliser la descente infinie...mais je me suis rendu compte qu'en montrant cela la descente infinie etait inutile car il est impossible que X-Y soit une puissance n 'eme car il ne contient qu'un seul "2" dans sa decomposition....
Bien Cordialement
Comme tu l'as dis Le theoreme de Fermat Wiles a deja eté demontré....mais la n'est pas la question, la question qui reste tout de meme , en tout cas pour moi d'actualité est "existe t-il une demonstration "elementaire" du theoreme de fermat" ?
Ayant obtenue ces droles d'equations je me suis dis que j'allais les presenter sur un forum afin de voir si cela a deja été demontré , et sinon quelqu'un a t-il une idée pour continuer et trouver une absurdité
Bien evidemment j'ai tenté de montrer que X-Y etait une puissance n'eme afin d'utiliser la descente infinie...mais je me suis rendu compte qu'en montrant cela la descente infinie etait inutile car il est impossible que X-Y soit une puissance n 'eme car il ne contient qu'un seul "2" dans sa decomposition....
Bien Cordialement
Je doute franchement qu'une preuve "élémentaire" (=avec des outils d'arithmétique qu'on connaissait à l'époque de Fermat) du théorème de Fermat-Wiles soit possible. Un peu d'humilité, songeons que des milliers de mahtématiciens professionnels et plus au fait de toutes les interconnexions entre les domaines des mathématiques y ont réfléchi avant nous...
Je Crois Bien Que Tu Fais La Une Erreur De Raisonnement Simon....
J'ai Un Grand Respect Envers Les Anciens Mathematiciens.....mais Regard Cette Exemple:
Un Etudiant Rentrant Dans Une Bibliotheque Cherchez Un Livre , En Sortant Il Dit A Son Ami Le Livre N'y Est Pas Simplement En Le Cherchant......la Phrase Correct Aurait Ete Je N'ai Pas Trouver Le Livre...mais Peut Etre Y Est T-il?
Ce Que Je Veux Te Dire C'est Qu'en Partant De L'equation De Fermat Je Tombe Sur Ces Equations....si Cela N'a Jamais Etait Montre Alors Cela Contredit Ce Que Tu Avance..
Cordialement.
A.a
J'ai Un Grand Respect Envers Les Anciens Mathematiciens.....mais Regard Cette Exemple:
Un Etudiant Rentrant Dans Une Bibliotheque Cherchez Un Livre , En Sortant Il Dit A Son Ami Le Livre N'y Est Pas Simplement En Le Cherchant......la Phrase Correct Aurait Ete Je N'ai Pas Trouver Le Livre...mais Peut Etre Y Est T-il?
Ce Que Je Veux Te Dire C'est Qu'en Partant De L'equation De Fermat Je Tombe Sur Ces Equations....si Cela N'a Jamais Etait Montre Alors Cela Contredit Ce Que Tu Avance..
Cordialement.
A.a
A.A a écrit:"existe t-il une demonstration "elementaire" du theoreme de fermat" ?
Le théorème de Fermat est inaccessible aux méthodes élémentaires (congruences...). Cela a été démontré et tu peux en trouver une preuve dans "Introduction to cyclotomic fields" de Washington. Il y a beaucoup d'autres livres accessibles sur ce sujet, notamment deux de Paulo Ribenboïm ("13 lectures sur le th. de F". et "FLT for amateurs") et un de Hellegouarch.
Il est avéré de toutes façons que la plus belle preuve du théorème de Fermat se trouve sur http://denisfeldmann.fr/humour.htm#ferm .
A.A a écrit:Donc D'apres Toi Il N'existe Pas De Demonstration Elementaire Du Theoreme De Fermat.....je Ne Sais Pas Comment Cela A Ete Demontre Mais Ces Raisonnements Prennent T-ils En Comptes Les Astuces De Calcul...? Cela M'etonnerai Un Peu...
Cordialement
Bonjour,
Veux-tu bien cesser d'écrire le début de chaque mot avec une majuscule! C'est non seulement contraire à la grammaire française, c'est aussi très agaçant!
Merci
Pour la modération
lapras a écrit:Yos > Comment montrer qu'on ne peut pas montrer quelquechose ? (dans un cas général, pas forcément le théoreme de fermat)
Abel et Galois ont bien prouvé qu'on ne pouvait pas résoudre par radicaux les équations de d°>4.
On peut prouver que
C'est de même nature non?
Dans les deux démos que j'évoque, il y a une similitude.
1) On prend tous les nombres réels qui s'écrivent avec des radicaux, ça fait un ensemble (un corps) assez petit en quelque sorte par rapport à l'ensemble des nombres algébriques.
2) De même on prend toutes les fonctions ayant une primitive ne s'écrivant qu'avec : constantes, x, cos x, sin x, ln x, et les opérations +-X: et o. Là encore on voit qu'on va pas loin avec ça.
et les opérations +-X: et o. Là encore on voit qu'on va pas loin avec ça.
Autre similitude : c'est assez long bien sûr.
1) On prend tous les nombres réels qui s'écrivent avec des radicaux, ça fait un ensemble (un corps) assez petit en quelque sorte par rapport à l'ensemble des nombres algébriques.
2) De même on prend toutes les fonctions ayant une primitive ne s'écrivant qu'avec : constantes, x, cos x, sin x, ln x,
Autre similitude : c'est assez long bien sûr.
Je savais que j'allais me faire grondé :we:
Je vais donc preciser ce que je voulais dire:
Tu affirme qu'il existe une demonstration qui prouve qu'il n'existe aucune demonstration elementaire du theoreme de Fermat.
Bien evidemment je n'utilise pas que les congruences( car la je suis d'accord on a peu de chance d'y arriver) mais j'utilise:
1)le petit theoreme de Fermat et les congruences
2)le theoreme de Gauss ainsi que ces lemmes
3)le theoreme fondamentale de l'arithmetique
4)Et des astuces de calcul.
d'ailleurs je ne sais pas si sa complique les choses mais j'ai tout de meme demontré que:
Le probleme de fermat est equivalent a dire: Il est impossible que:
Z-Y soit une puissance n eme et (Z^n-Y^n)/(Z-Y) soit aussi une puissance n eme .
Il evident que la condition est necessaire et d'aprés mes resultats elle devient suffisante....
cordialement
Je vais donc preciser ce que je voulais dire:
Tu affirme qu'il existe une demonstration qui prouve qu'il n'existe aucune demonstration elementaire du theoreme de Fermat.
Bien evidemment je n'utilise pas que les congruences( car la je suis d'accord on a peu de chance d'y arriver) mais j'utilise:
1)le petit theoreme de Fermat et les congruences
2)le theoreme de Gauss ainsi que ces lemmes
3)le theoreme fondamentale de l'arithmetique
4)Et des astuces de calcul.
d'ailleurs je ne sais pas si sa complique les choses mais j'ai tout de meme demontré que:
Le probleme de fermat est equivalent a dire: Il est impossible que:
Z-Y soit une puissance n eme et (Z^n-Y^n)/(Z-Y) soit aussi une puissance n eme .
Il evident que la condition est necessaire et d'aprés mes resultats elle devient suffisante....
cordialement
Salut,
Une version possible du théorème de Fermat :
tu as raison.
Je vais te montrer que tu ne pourras pas prouver le théorème de Fermat avec uniquement ça : ce que tu utilises ici, ce sont uniquement les propriétés d'un anneau principal (et disons aussi les "astuces" qu'on peut y développer).
Or il y a des anneaux principaux où le résultat est faux : dans R[t] l'anneau des polynômes en t à coefficients réels. Cet anneau est principal, ok.
Malheureusement pour le théorème de Fermat, dans cet anneau principal, il y a bcp de contre-exemples à l'énoncé car bcp d'éléments sont des racines n-ième (à cause de R).
Exemple bête pour tout n :^n + (1+t)^n = \big( 2^{1/n} (1+t) \big)^n)
et pourtant ni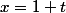 , ni
, ni 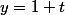 , ni
, ni ) ne sont nuls...
ne sont nuls...
Conclusion : pour démontrer le théorème de Fermat, il faut utiliser une propriété de Z qui sort du contexte anneau principal.
Une version possible du théorème de Fermat :
Soitet un exposant
.
Sialors
.
A.A a écrit:Je vais donc preciser ce que je voulais dire:
tu as raison.
A.A a écrit:Tu affirme qu'il existe une demonstration qui prouve qu'il n'existe aucune demonstration elementaire du theoreme de Fermat.
Bien evidemment je n'utilise pas que les congruences( car la je suis d'accord on a peu de chance d'y arriver) mais j'utilise:
1)le petit theoreme de Fermat et les congruences
2)le theoreme de Gauss ainsi que ces lemmes
3)le theoreme fondamentale de l'arithmetique
4)Et des astuces de calcul.
Je vais te montrer que tu ne pourras pas prouver le théorème de Fermat avec uniquement ça : ce que tu utilises ici, ce sont uniquement les propriétés d'un anneau principal (et disons aussi les "astuces" qu'on peut y développer).
Or il y a des anneaux principaux où le résultat est faux : dans R[t] l'anneau des polynômes en t à coefficients réels. Cet anneau est principal, ok.
Malheureusement pour le théorème de Fermat, dans cet anneau principal, il y a bcp de contre-exemples à l'énoncé car bcp d'éléments sont des racines n-ième (à cause de R).
Exemple bête pour tout n :
et pourtant ni
Conclusion : pour démontrer le théorème de Fermat, il faut utiliser une propriété de Z qui sort du contexte anneau principal.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
