Le Dernier Théorème de Fermat. Preuve pour lycéens
55 messages
- Page 3 sur 3 - 1, 2, 3
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Une erreur. Dans le théorème de Fermat n > 2.
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Victor Sorokine a écrit:Une erreur. Dans le théorème de Fermat n > 2.
Bonsoir,
1) Pardon!Il n'y a pas d'erreur , dans mon raisonnement!Pour n=2 , l'équation
2) Démontrer , s'il vous plaît , votre déclaration "Le nombre
3) Comment résolvez-vous dans l'ensemble
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Dacu a écrit:Victor Sorokine a écrit:Une erreur. Dans le théorème de Fermat n > 2.
Bonsoir,
1) Pardon!Il n'y a pas d'erreur , dans mon raisonnement!Pour n=2 , l'équationa des solutions , parce que
a des solutions dans l'ensamble
.
2) Démontrer , s'il vous plaît , votre déclaration "Le nombren'est pas divisible par
." où
!
3) Comment résolvez-vous dans l'ensembleou
l'équation
et par exemple pour
, quelles sont les solutions?Merci!
Cordialement,
Dacu
Si
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Victor Sorokine a écrit:Dacu a écrit:Victor Sorokine a écrit:Une erreur. Dans le théorème de Fermat n > 2.
Bonsoir,
1) Pardon!Il n'y a pas d'erreur , dans mon raisonnement!Pour n=2 , l'équationa des solutions , parce que
a des solutions dans l'ensamble
.
2) Démontrer , s'il vous plaît , votre déclaration "Le nombren'est pas divisible par
." où
!
3) Comment résolvez-vous dans l'ensembleou
l'équation
et par exemple pour
, quelles sont les solutions?Merci!
Cordialement,
Dacu
Si, où
n'est pas divisible par
, alors
n'est pas divisible par 3.
Bonjour,
1) Comment résolvez-vous dans l'ensemble
2) Mais , pour
3)
4) Peut être
Merci beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Je n'ai toujours pas compris ce qui se passe lorsque (ABC)'=0. Dans ce cas, C-B, C, B et n ne sont pas premiers entre eux en général, d'où C-B et P ne sont pas premiers entre eux, et donc le 2 de la nouvelle preuve en deux opérations ne tient pas. Cela est il une erreur fondamentale? Comment fait on?
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Dacu a écrit:
1) Comment résolvez-vous dans l'ensembleou
l'équation
?On peut écrire que
où
et
?
2) Mais , pourou
,
....... ?
3)peut être divisible par
?
4) Peut êtreavec
et
où
?
Si D est divisible par n, alors P est divisible par n et les deux C et B sont divisibles par n. Par conséquent, le C-B est divisé par n. Mais les nombre C-B n’est divisé pas par n !
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Pafapafadidel a écrit:Je n'ai toujours pas compris ce qui se passe lorsque (ABC)'=0. Dans ce cas, C-B, C, B et n ne sont pas premiers entre eux en général, d'où C-B et P ne sont pas premiers entre eux, et donc le 2 de la nouvelle preuve en deux opérations ne tient pas. Cela est il une erreur fondamentale? Comment fait on?
Si B'=0, alors C-B, C, B sont premiers entre eux, C-B n’est divisé pas par n et P n’est divisé pas par n.
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Le premier cas du dernier théorème de Fermat est prouvé.
Une belle preuve de 4 lignes du lemme se trouve:
Dans l'équation de Fermat de base dans le premier cas [ n'est pas divisible par n] les nombres P, Q, R [dans les égalités
n'est pas divisible par n] les nombres P, Q, R [dans les égalités 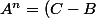P) ,
, Q) ,
, R=c^nr^n) ] ont une fin de trois chiffres 001. Et, par conséquent, les nombres A, B, C sont infiniment grands (voir http://vixra.org/abs/1707.0092).
] ont une fin de trois chiffres 001. Et, par conséquent, les nombres A, B, C sont infiniment grands (voir http://vixra.org/abs/1707.0092).
En effet, par exemple, tout facteur prime du nombre R° dans l'égalité^n+(C-A)^n=a^{nn}+b^{nn}=(a^n+b^n)R) ° a, selon Lemme 6°, une fin de deux chiffres 01.
° a, selon Lemme 6°, une fin de deux chiffres 01.
Et tout facteur premier du nombre R est un facteur du nombre D, mais ce n'est pas un facteur du nombre (puisque les nombres A+B et R sont relativement premiers).
(puisque les nombres A+B et R sont relativement premiers).
Une belle preuve de 4 lignes du lemme se trouve:
Dans l'équation de Fermat de base dans le premier cas [
En effet, par exemple, tout facteur prime du nombre R° dans l'égalité
Et tout facteur premier du nombre R est un facteur du nombre D, mais ce n'est pas un facteur du nombre
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Supposons que l'on est dans le premier cas du dernier théorème de Fermat. Peux tu expliquer pourquoi A_[2]=a^n_[2 (c'est à dire l'étape 4-1)? Je ne vois pas quelle est la preuve de cela, étant donné que l'on sait seulement que A=ap.
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Pafapafadidel a écrit:Supposons que l'on est dans le premier cas du dernier théorème de Fermat. Peux tu expliquer pourquoi A_[2]=a^n_[2 (c'est à dire l'étape 4-1)? Je ne vois pas quelle est la preuve de cela, étant donné que l'on sait seulement que A=ap.
Cela découle de
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Personnellement, autant le fait que  (*) me semble parfaitement clair vu que
(*) me semble parfaitement clair vu que  , autant je ne vois aucune raison particulière pour que
, autant je ne vois aucune raison particulière pour que  .
.
Et je rajouterais que j'ai pas franchement l'intention de perdre mon temps à chercher pour voir si cette affirmation et effectivement juste ou pas (pas plus que les suivantes) : il faut bien que tu réalise que tu est le je-sais-pas-combien-ième à penser à avoir trouvé une preuve et que jusque là, elles étaient toutes fausses. Donc, a mon avis, tu ne trouvera personne de sérieux qui ait envie de perdre son temps à tenter de boucher les trous de ta preuve incomplète.
Bref,
- Soit tu rédige TOUT sans exception (et si possible correctement, c'est à dire avec les notations usuelles des matheux concernant les congruences et pas des notations farfelues)
- Soit il faut t'attendre très clairement à ce qu'aucune personne compétente ne lise jamais ton truc.
(*) A + B congru à C modulo n
Et je rajouterais que j'ai pas franchement l'intention de perdre mon temps à chercher pour voir si cette affirmation et effectivement juste ou pas (pas plus que les suivantes) : il faut bien que tu réalise que tu est le je-sais-pas-combien-ième à penser à avoir trouvé une preuve et que jusque là, elles étaient toutes fausses. Donc, a mon avis, tu ne trouvera personne de sérieux qui ait envie de perdre son temps à tenter de boucher les trous de ta preuve incomplète.
Bref,
- Soit tu rédige TOUT sans exception (et si possible correctement, c'est à dire avec les notations usuelles des matheux concernant les congruences et pas des notations farfelues)
- Soit il faut t'attendre très clairement à ce qu'aucune personne compétente ne lise jamais ton truc.
(*) A + B congru à C modulo n
Modifié en dernier par Ben314 le 07 Oct 2017, 13:15, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Ben314 a écrit:Bref,
- Soit tu rédige TOUT sans exception (et si possible correctement, c'est à dire avec les notations usuelles des matheux concernant les congruences et pas des notations farfelues)
- Soit il faut t'attendre très clairement à ce qu'aucune personne compétente ne lise jamais ton truc.
Toutes les propriétés les plus simples de l'égalité de base sont connues depuis 300 ans et leur preuve est:
http://vixra.org/pdf/1707.0092v1.pdf
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Si tu considère que d'affirmer que "les propriétés 1° à 5° sont connues" constitue une preuve, et bien ne t'étonne pas que personne ne lise ton truc (*).Victor Sorokine a écrit:Toutes les propriétés les plus simples de l'égalité de base sont connues depuis 300 ans et leur preuve est:
http://vixra.org/pdf/1707.0092v1.pdf
Si tu as la flemme de refaire les preuve en question et qu'effectivement c'est "connu", ben tu fait... ce que tout scientifique fait, à savoir que tu donne des références précises : Livre ou Article + Auteur + Date + N° de la page où la propriété que que tu utilise est énoncée. (en Français, ça s'appelle une "bibliographie")
Et ça sera ma dernière intervention : perso, je m'en fout complètement de ton truc (vu que je suis certain que c'est faux) et si tu n'a pas envie de faire les efforts nécessaires pour que certaines personnes compétentes relisent ton laïus, c'est toi et toi seul que ça regarde.
(*) Et je rajouterais que, quand on te demande d'où sort un résultat, par exemple le fait que A+B=C [n²], que la seule chose que tu soit capable de répondre soit "c'est connu depuis 300 ans" et cela sans donner aucune référence ne laisse rien présager de bon concernant la façon dont tu voit les choses (i.e. que tu considère que c'est au lecteur de se démerder pour trouver les références...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
Ici: http://vixra.org/pdf/1707.0092v1.pdf
il y a une preuve de chaque déclaration.
il y a une preuve de chaque déclaration.
Re: Le Dernier Théorème de Fermat. Preuve pour lycéens
je t'ai déjà dit que NON, il n'y a pas de preuves dans ton truc.Victor Sorokine a écrit:Ici: http://vixra.org/pdf/1707.0092v1.pdf
il y a une preuve de chaque déclaration.
Par exemple l'affirmation 4a-I°)
Bref, ton truc est, comme tant d'autres, sans le moindre intérêt dans sa forme actuelle.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
55 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
