Le Dernier Théorème de Fermat. Preuve en 2 opérationsL'égalité de Fermat est contradictoire entre les deuxièmes chiffres des facteurs du nombre A.
Tous les nombres entiers sont traités dans un système numérique avec une base

, où

est un nombre premier supérieur à

.
Notations :
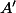
,
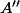
– premier, deuxième chiffre à partir de la fin du nombre

;
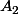
– la terminaison de 2 chiffres du nombre

(où

mod

);
Nous considérons l'égalité de Fermat dans le cas de base (ses propriétés sont prouvées ici:
http://vixra.org/abs/1707.0092) pour les entiers naturels (premiers entre eux)

,

,

;
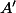
≠

et

nombre premier
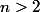
:
1°)
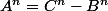
[
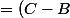P)
], où (comme on le sait)
2°)
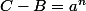
,
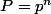
,
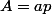
,
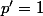
,
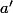
≠

,
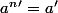
,
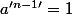
(petit théorème de Fermat);
3°)
_2=0)
, d'où
3a°)
_2=a^n_2)
et, par conséquent,
3b°)
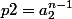
4°) Si
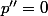
, alors nous multiplions le terme par le terme l'égalité 1° par
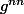
tel que
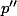
≠

.
En outre, les propriétés 2°-3° sont conservées, et nous laissons la notation des nombres comme précédemment.
Et maintenant, la Preuve proprement dite du DTF Nous représentons les terminaisons
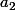
et
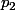
dans la forme:
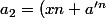_2)
et
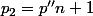
, où

est un chiffre.
D'abord, nous substituons ces valeurs des terminaisons dans la partie gauche de l'égalité 3a°:
5°)
(p''n+1)]_2=a'n_2)
, d'où
5a°)
_2=0)
, ou (см. 2°)
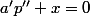
(mod

)
Maintenant, nous substituons la valeur de
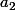
dans le côté droit de l'égalité 3b° :
6°)
^{n-1}_2=[(n-1)xna'^{n-2}+1]_2=(-nxa'^{n-2}+1)_2=(-nxa'^{n-1}/a'+1)_2)
Et de 3b° nous trouvons que :
6a°)
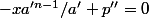
(mod

), ou
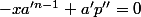
(mod

), ou
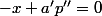
(mod

).
Il résulte de 5a° et 6a° que
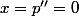
, ce qui contredit à 2° et 4°.
Par cette contradiction le DTF est vérifié.
(Mézos, France. Le 4 septembre 2017)

