Le Grand Théorème de Fermat
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Mar 2013, 18:07
par Dacu » 10 Mar 2013, 18:07
Bonsoir!
Milliers d'excuses !J'ai posté quelque chose qui ne correspond pas à ce sujet.
Ajustement :
Grand Theoreme de Fermat a des solutions dans l'ensemble des nombres complexes ?
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 10 Mar 2013, 18:12
par Kikoo <3 Bieber » 10 Mar 2013, 18:12
Salut,
A première vue, cela me semble étrange, il n'existe pas de relation d'ordre usuelle sur l'ensemble des complexes.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Mar 2013, 18:41
par Dacu » 10 Mar 2013, 18:41
Kikoo <3 Bieber a écrit:Salut,
A première vue, cela me semble étrange, il n'existe pas de relation d'ordre usuelle sur l'ensemble des complexes.
Milliers d'excuses !S'il vous plaît lire le premier post !Merci beaucoup!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 10 Mar 2013, 18:44
par Kikoo <3 Bieber » 10 Mar 2013, 18:44
Allier arithmétique et nombres complexes je pense que ça s'est déjà fait dans des cadres particuliers, et sur des ensembles particuliers.
Mais cela me dépasse complètement ^^ Je vais laisser d'autres personnes en discuter. Et pense à modifier ton titre pour que l'on sache que ça a aussi un lien avec les complexes.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Mar 2013, 18:46
par Nightmare » 10 Mar 2013, 18:46
Si x et y sont fixés, alors quel que soit n il existera toujours un racine n-ème complexe à x^n+y^n donc il existera toujours z tel que x^n+y^n=z^n
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Mar 2013, 19:00
par Dacu » 10 Mar 2013, 19:00
Nightmare a écrit:Si x et y sont fixés, alors quel que soit n il existera toujours un racine n-ème complexe à x^n et y^n donc il existera toujours z tel que x^n+y^n=z^n
Correctement!Grand Theoreme de Fermat a des solutions dans l'ensemble des nombres rationnels ?
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Mar 2013, 19:26
par Nightmare » 10 Mar 2013, 19:26
S'il avait des solutions rationnelles il en aurait des entières en multipliant par un nombre bien choisi pour annuler les dénominateurs.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Mar 2013, 19:32
par Dacu » 10 Mar 2013, 19:32
Pour quelles valeurs de
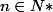
et

dont les parties réelles et imaginaires sont premiers entre eux et not null , Grand Theoreme de Fermat a des solutions?
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Mar 2013, 19:37
par Dacu » 10 Mar 2013, 19:37
Nightmare a écrit:S'il avait des solutions rationnelles il en aurait des entières en multipliant par un nombre bien choisi pour annuler les dénominateurs.
Je ne comprends pas ce que vous voulez dire !Détailler s'il vous plaît !
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 10 Mar 2013, 21:11
par Archytas » 10 Mar 2013, 21:11
Dacu a écrit:Je ne comprends pas ce que vous voulez dire !Détailler s'il vous plaît !
Ce qu'il veut dire c'est que si
^n + (\frac{p'}{q'})^n = (\frac{p''}{q''})^n)
alors
^n+(p'qq'')^n=(p''qq')^n)
ce qui est impossible, non ?
PS : J'imagine que tu es anglais, on dit
le grand théorème de fermat (= !
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Mar 2013, 21:25
par Dacu » 10 Mar 2013, 21:25
Archytas a écrit:Ce qu'il veut dire c'est que si
^n + (\frac{p'}{q'})^n = (\frac{p''}{q''})^n)
alors
^n+(p'qq'')^n=(p''qq')^n)
ce qui est impossible, non ?
PS : J'imagine que tu es anglais, on dit
le grand théorème de fermat (= !
Correctement pour
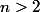
!Je ne suis pas anglais.Mon nom, dit ce que je suis.Pour quelles valeurs de
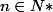
et

dont les parties réelles et imaginaires sont premiers entre eux et not null , Le Grand Théorème de Fermat a des solutions?
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 15 Mar 2013, 07:31
par Dacu » 15 Mar 2013, 07:31
Bonjour !
J'ai fait une extension des nombres complexes dans Le Grand Théorème de Fermat et j'espère que ce n'est pas mal.
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 05 Avr 2013, 06:35
par Dacu » 05 Avr 2013, 06:35
N'est plus est-ce quelqu'un s'intéresse à cette question ? :triste:
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 05 Avr 2013, 16:23
par Dacu » 05 Avr 2013, 16:23
Bonsoir!
Considérons la fonction
=\alpha ^n)
où
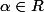
,
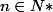
et
)
est continue en tout point de

et

,
)
est dérivable en tout point de

et

, alors comme conséquence du théorème de la moyenne de Lagrange , nous pouvons écrire
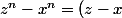 \cdot f^'(c_{zx}))
et
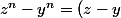 \cdot f^'(c_{zy}))
où

,

et

.Quelles relations on peut écrire sachant que
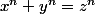
?
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 05 Avr 2013, 18:22
par Imod » 05 Avr 2013, 18:22
Ca part un peu dans tous les sens , sans savoir ce que l''on cherche , il ne faut pas s'étonner que personne ne participe :zen:
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
alors
ce qui est impossible, non ?
=\alpha ^n) où
où 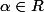 ,
, 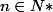 et
et ) est continue en tout point de
est continue en tout point de  et
et  ,
, ) est dérivable en tout point de
est dérivable en tout point de  et
et  , alors comme conséquence du théorème de la moyenne de Lagrange , nous pouvons écrire
, alors comme conséquence du théorème de la moyenne de Lagrange , nous pouvons écrire 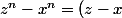 \cdot f^'(c_{zx})) et
et 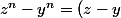 \cdot f^'(c_{zy})) où
où  ,
,  et
et  .Quelles relations on peut écrire sachant que
.Quelles relations on peut écrire sachant que 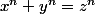 ?
?