Calcul intégral par la méthode des résidus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 12:24
par mehdi-128 » 28 Déc 2007, 12:24
Bonjour,je bloque sur le calcul de cette intégrale:
}{1-2a\cos(t)+a^2} dt)
ou : /a/ différent de 1 ....
Et on me dit:indication:
On pourra calculer le long du cercle unité:
(z-\frac{1}{a}))
Et déja je vois pas trop comment faire pour l'indication.....
merci d'avance ....
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 13:04
par trust » 28 Déc 2007, 13:04
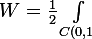}(blablabla)
//avec chgt de var en complexe
 \frac {dz}{iz} = 2i\pi res(blablabla,pole))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 13:21
par mehdi-128 » 28 Déc 2007, 13:21
trust a écrit: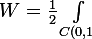}(blablabla)
//avec chgt de var en complexe
 \frac {dz}{iz} = 2i\pi res(blablabla,pole))
Franchement j'ai rien compris a ce que tu m'as mis :triste:
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 13:32
par mehdi-128 » 28 Déc 2007, 13:32
J'ai remarqué que:
)(a-exp(-it))=a^2-2a\cos(t)+1)
donc :
(a-\frac{1}{z})} dz)
en effectuant le changement de variable:
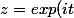)
Et la je bloque .....
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 14:27
par trust » 28 Déc 2007, 14:27
bah applique le théorème des résidus dans les calculs d'intégral, cherche le pôle de la fonction méromorphe où la partie imaginaire est positive, calcule le résidu en ce point puis applique la formule que je t'ai donnée...
c'est de l'analyse complexe en fait, un truc chiant mais qui simplifie pas mal de calculs comme ici ==>
http://www.maths-forum.com/showthread.php?p=321560#post321560 <==
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 14:42
par mehdi-128 » 28 Déc 2007, 14:42
trust a écrit:bah applique le théorème des résidus dans les calculs d'intégral, cherche le pôle de la fonction méromorphe où la partie imaginaire est positive, calcule le résidu en ce point puis applique la formule que je t'ai donnée...
c'est de l'analyse complexe en fait, un truc chiant mais qui simplifie pas mal de calculs comme ici ==>
http://www.maths-forum.com/showthread.php?p=321560#post321560 <==
Et pourquoi faut-il que la partie imaginaire soit positive ?
J'ai jamais entendu parlé de ça .....
c'est quoi une fonction méromorphe ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 14:45
par mehdi-128 » 28 Déc 2007, 14:45
Sinon ,ici j'ai 3 poles: 0,a et 1/a
mais comment calculer le résidu en 0, a et 1/a ?
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 14:46
par trust » 28 Déc 2007, 14:46
t'as bien suivi des cours d'analyse complexe non? pour pouvoir calculer un intégral par la méthode des résidus?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 14:51
par mehdi-128 » 28 Déc 2007, 14:51
trust a écrit:t'as bien suivi des cours d'analyse complexe non? pour pouvoir calculer un intégral par la méthode des résidus?
oui mais j'avais des cas simples :Res(p/q,z0)=p(z0)/q'(z0)
avec p et q 2 fonctions holomorphes dans un voisinage de z0 tq z0 soit zéro simple de q(z) et p(z0) different de 0....
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 15:12
par mehdi-128 » 28 Déc 2007, 15:12
Et déja ,on sait juste que a n'est pas sur le cercle ,mais on ne sait pas s'il est a l'intérieur ou pas donc comment calculer son indice ?
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 15:41
par trust » 28 Déc 2007, 15:41
t'as qu'à considérer les 2 cas : si a est dans le cercle, l'indice vaut 1 sinon 0 à l'extérieur...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 15:44
par mehdi-128 » 28 Déc 2007, 15:44
trust a écrit:t'as qu'à considérer les 2 cas : si a est dans le cercle, l'indice vaut 1 sinon 0 à l'extérieur...
Ok donc je le considère a l'intérieur:
J'ai :
=\frac{a^n+a^{-n}}{1-a^2})
=\frac{a^n+a^{-n}}{a^2-1})
Je trouve donc:

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 16:06
par mehdi-128 » 28 Déc 2007, 16:06
trust es-tu d'accord avec moi ?
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 16:32
par trust » 28 Déc 2007, 16:32
mouep, ça a l'air juste quoi que si

est dans le cercle,

ne l'est pas et ça me chagrine un peu, donc distingue les 2 cas dans tes solutions.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 17:04
par mehdi-128 » 28 Déc 2007, 17:04
trust a écrit:mouep, ça a l'air juste quoi que si

est dans le cercle,

ne l'est pas et ça me chagrine un peu, donc distingue les 2 cas dans tes solutions.
ah oui j'avais oublié ,quel étourdi !!
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 17:05
par mehdi-128 » 28 Déc 2007, 17:05
1er cas: si abs(a)1
l'indice de a vaut 1 celui de 1/a vaut 0 j'obtiens:
}{2(1-a^2)})
Pour le 2eme cas j'obtiens la meme chose avec un signe moins ....[/quote]
Ca semble correct ?
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 17:18
par trust » 28 Déc 2007, 17:18
détaille un peu pour voir...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 17:27
par mehdi-128 » 28 Déc 2007, 17:27
trust a écrit:détaille un peu pour voir...
D'après le théorème des résidus:
pour le 1er cas: si abs(a)1
d'ou :Ind(a)=1 et Ind(1/a)=0
d'après le théorème des résidus:
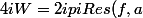)
d'ou:
}{2(1-a^2)})
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 17:29
par trust » 28 Déc 2007, 17:29
d'ou vient ce

?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 17:49
par mehdi-128 » 28 Déc 2007, 17:49
trust a écrit:d'ou vient ce

?
cos(t) =exp(it)+exp(-it) / 2
et le 2 issu de int [0..Pi]=1/2 . int[C(0,1)] ....
2*2=4 ....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités