Mesure de comptage !

[legeniedesalpages]

j'avais mal lu l'énoncé, mais j'ai modifié en fonction, est bien dans , car ou bien il est fini ou bien son complémentaire dans N est fini.

[barbu23]

non le complementaire n'est pas fini prends par exemple l'ensemble des entiers pairs, il est infini mais son complementaire est l'ensemble des entiers impair qui n'est pas fini !!

[legeniedesalpages]

ah non oui effectivement il y a un problème.

[legeniedesalpages]

non le complementaire n'est pas fini prends par exemple l'ensemble des entiers pairs, il est infini mais son complementaire est l'ensemble des entiers impair qui n'est pas fini !!

Oui mais cet ensemble donc pas dans ,
ici on veut unir deux éléments de .

Soient .

Si A est fini et B est fini, leur union est finie et donc dans .

Si A est fini et B est infinie est infini car contient B,cependant son complémentaire , qui est fini car B est infini et est dans donc son complémentaire est fini.

On procède de la même façon si A est infini et B est fini.
Et on procède aussi de même en étudiant les complémentaires de A et B dans le cas où ils sont tous les deux infinis.

[barbu23]

non si est infini dans 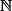ça ne veut pas dire que son complementaire est fini ... ! je pense que c'est ça l'idée ce que tu as fait mais ... il faut passer par les 4 cas que j'ai cité dans un message precedent et là je pense qu'on peut arriver !! mais c'est exactement comme ça qu'il faut raisonner je pense !!

[barbu23]

Pour le cas et le cas il n'y'a pas de problème !!! mais pour et c'est le meme raisonnement que ce que tu as fait tout à l'heure !!

[legeniedesalpages]

non si est infini dans ça ne veut pas dire que son complementaire est fini ... ! je pense que c'est ça l'idée ce que tu as fait mais ... il faut passer par les 4 cas que j'ai cité dans un message precedent et là je pense qu'on peut arriver !! mais c'est exactement comme ça qu'il faut raisonner je pense !!

Dans ton message n°35, tu as dit que

Donc pour tout élément , par définition soit A est fini soit est fini.

Donc si est infini, c'est que est fini.

Je vois pas où le problème. On veut montrer que est stable par union finie, donc on prend deux éléments de qui eux respectent toujours cette condition.

[legeniedesalpages]

D'ailleurs on peut même prouver que est une tribu.

[barbu23]

oui, tu as raison !!

[barbu23]

Comment faire pour montrer que c'est une tribu ? on a montré que c'est un clan !! il reste le clan et l'unitarité !!
Pour l'unitarité c'est simple car est fini.
Pour le clan :
On prend une suite d'éléments deux à deux disjoints , il faut montre que la reunion denombrable est dans ...

[legeniedesalpages]

lol, je connais pas tous ces termes exotiques, pour moi une tribu ça vérifie 3 points:

1) et sont dans (facile à voir),

2) Stabilité par passage au complémentaire, facile à voir aussi.

3)Stabilité par union dénombrable (un peu plus subtil):

Soit une famille dénombrable de .

Si il existe tel que est infini, alors est fini, et donc

est fini.

Je cherche pour el cas où tous les sont finis.

[legeniedesalpages]

Non oui d'ailleurs, c'est pas une tribu, je me suis trompé, désolé.

On prend , l'union des est l'ensemble des entiers pairs qui n'est pas dans .

[legeniedesalpages]

J'avais confondu avec un autre exo:

est une tribu sur .

[barbu23]

Est ce que la fonction d'ensembles suivante :

.
est additive ?
Dans le cours elle n'est pas additive !!

[barbu23]

C'est à cause de ça, non :
Si on prend une suite denombrable d'elements dans la reunion denombrables de ces elements ne sont pas dans ... c'est ça ? par définition !!

[legeniedesalpages]

oui ça ne marche pas,

si tu prends , pour tout entier n, _n est une suite disjointe d'éléments de .

Tu vois que (car est infini).

Cependant pour tout n, (car est fini), donc .

Il est donc clair que .

Au passage dans cet exemple, l'union est dans , mais ça ne marche quand même pas.

[barbu23]

Bonjour :
Je cherche une suite de fonctions mesurables positives non étagées dont le produit est convergent !!
Tout ça pour voir ce qui va se passer à la mesure suivante à l'infini :
( Est ce que ça va rester une mesure ou bien non ?! )

Merci de votre reponse !!

[barbu23]

Normalement la limite d'une suite croissante de mesures est une mesure !! mais ici, est ce que est croissante ?

[barbu23]

n'est croissante que si les
Donc est une mesure si on suppose que les elements de la suite sont !!
Donc : est une mesure, même si le produit diverge !!