Suites adjacentes et limite commune...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 14 Sep 2007, 20:32
par pouik » 14 Sep 2007, 20:32
Bonsoir,
J'aimerai savoir si ce que j'ai fait est correct et si vous pouviez m'aider à résoudre la partie que je n'ai su fzaire, ce serait vraiment formidable.
Merci d'avance.
Soient

et

deux réels tels que
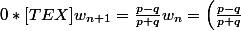^{n+1}(q-p))
donc
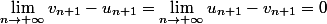
*
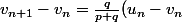 = q \times \left(\frac{p-q}{p+q}\right)^{n+1})
donc
)
est croissante.
*
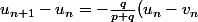 = -q \times \left(\frac{p-q}{p+q}\right)^{n+1})
donc
)
est décroissante.
Les 2 suites sont donc adjacentes et convergent donc vers la même limite

,
mais arrivé là je n'y arrive plus du tout... :hum:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 14 Sep 2007, 20:36
par fahr451 » 14 Sep 2007, 20:36
bonsoir
je n'ai pas vérifié les calculs mais ça semble correct
je présume qu 'il te manque la valeur de la limite
et si tu faisais u(n+1) +v(n+1) ....?
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 15 Sep 2007, 13:01
par pouik » 15 Sep 2007, 13:01
Je trouve donc que :
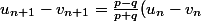)
mais après je ne vois pas quoi faire car exploiter ici le fait que la différence tend vers 0 n'aboutit pas ! :doh:
Merci d'avance pour votre aide.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 13:02
par fahr451 » 15 Sep 2007, 13:02
++++++++++++ et non différence
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 15 Sep 2007, 13:17
par pouik » 15 Sep 2007, 13:17
Je trouve que
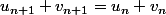
mais bon là je vois pas non plus quoi faire car un passage à la limite nous dirait que
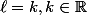
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 13:27
par fahr451 » 15 Sep 2007, 13:27
que dire de la suite u +v ??
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 15 Sep 2007, 13:37
par pouik » 15 Sep 2007, 13:37
elle est constante, donc :
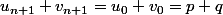
or
 \rightarrow \ell)
et
 \rightarrow \ell)
donc par passage à la limite dans l'égalité précédente, on obtient :
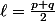
Non ??
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 13:38
par fahr451 » 15 Sep 2007, 13:38
ma foi on dirait bien
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 15 Sep 2007, 13:52
par pouik » 15 Sep 2007, 13:52
merci beaucoup :zen: :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
