Topologie (révision)

[sandrine_guillerme]

Bonjour,
comme par exemple la topologie decrite ici...

merci pour ton lien,

mais je le trouve dur, j'ai pas compris grand choses ..

[legeniedesalpages]

Salut la topologie de Zariski est définie par les fermés.

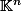
Je ne sais pas ce qu'entend alben par le cas général, je ne l'ai appris que sur , étant un corps.

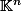
Sur , les fermés de Zariski sont les lieux des zéros de fonctions polynômiales à n-variables (très exotique à mon goût :lol2:)

[sandrine_guillerme]

Les lieux ? euh .. en se situant où? et par rapport à quoi?

[legeniedesalpages]

Je ne sais pas où tu en es en topologie, mais je pense qu'il y a pas mal de choses à voir avant l'espace des fonctions tests :ptdr:

Tu en es où en topologie? T'est tu familiarisée avec la topo grossière, discrète, métrique, quotient, induite, produit ??
Je pense que ce sont les premières à rencontrer.

[sandrine_guillerme]

bah, je passe en L3 math

tout ce que je connais en topo pour l'instant c'est :

Les espaces mètriques
Les espaces normées .
Calcul différentiel

[legeniedesalpages]

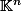
ok, ben on prends l'ensemble où est un corps.
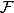
On note l'ensemble des fonctions polynomiales à n variables.

l'ensemble des fermés de Zariski est avec pour tout ensemble , .

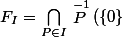Du moins il me semble que c'est ça, vu le peu d'utilité de cette topologie que j'en ai eu, je ne me suis pas attardé dessus, c'est juste pour la culture (à moins peut être pour ceux qui font de la topologie algébrique)

[legeniedesalpages]

oui les espaces métriques et normés sont les plus importants même en L3. En L3 on se familiarise plus (vite fait) avec les outils et les raisonnements intrinsèques à la topologie comme la compacité, la complétude, la connexité...

[sandrine_guillerme]

merci pour ces informations ..

Tu peux me définir stp ce que veux dire qu'une topologie plus fine qu'une autre ?
la référence que j'ai dis que c'est vrai ssi les ouverts de la deuxième (moins fine) sont des ouverts de la première (plus fine)


et sincèrement, je me sens vraiment perdu, c'est comme si j'y comprend rien, j'ai pas encore gouté le truc, c'est normal ?

Merci

[legeniedesalpages]

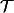
oui sur un ensemble , une topologie est plus fine qu'une topologie si .

La topologie grossière est la moins fine possible (on peut pas avoir moins d'ouverts vu la définition d'une topologie).

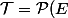La topologie discrète est la plus fine possible (il est clair qu'on peut pas avoir plus d'ouverts dans une topologie)

En général on travaille sur des espaces suffisamment fins pour qu'il soient séparés.

Oui la topologie ça peut mettre du temps à rentrer. J'ai eu du mal au début pendant pas mal de temps et je crois que c'est pareil pour pas mal de monde. Il faut être très familiarisé à manipuler des ensembles déjà. Ensuite ça reste assez abstrait. Puis en s'enfonçant dans la topologie, et en se cassant la tête sur des exos ça finit par rentrer. Il est bon de s'assister d'un cours, au moins on suit un fil directeur, c'est quand même mieux que de se paumer de lien en lien dans wiki :lol2:.

Perso j'utilise le Cours de topologie de Gustave Choquet qui est vraiment pas mal.

[legeniedesalpages]

Là, par exemple, il y a pas mal d'exos: http://labomathlens.free.fr/Liens/ExosTopoL2.pdf

[sandrine_guillerme]

Donc là ce que tu veux dire il faut et il suffit qu'une topologie soit incluse dans l'autre pour dire que cette dernière est plus fine ?

Question bête: Quelle est l'utilité des espaces séparés ?

Sinon moi j'utilise le cours d'une copine magnifique ( :zen: ) ... et d'un copain (les deux demath forum :zen: )
et un bouquin (la géométrie du caouatchouc)

C'est vrai que j'ai du mal, vraiment du mal,

mais il faut que je m'accroche,


T'es en M1 toi?

[legeniedesalpages]

Déjà un espace séparé permet d'avoir au plus une limite pour une suite convergente, ce qui est plutôt sympa.

EDIT: non je suis postier, j'avais arrêté les études cette année, mais là je reprends en L3 comme toi en septembre.

[sandrine_guillerme]

Ok, C'est sympa oui..

sinonJe laisse reposer le site que tu m'as donné telle une pâte à crêpe ..

Parceque maintenant Je dois au mois comprendre les 4 ou 5 permiers chapitres .. dans ce cas là, je pourrais commencer les exos pour mieux comprendre quoi ..

huh ! :doh: Tu sais que t'es largement en avance ? Ton L3 tu la fera où?

[legeniedesalpages]

je me suis pas trop renseigné sur les programmes, mais vaut mieux que je sois un peu avance parce que l'année prochaine ej serai encore postier :lol2:.
Enfin à mon avis j'ai pas tant d'avance que moi (les dérivées, les corps, et l'intégration, il y a encore pas mal de boulot je pense)
Je ferai ma L3 à montpellier.

EDIT: toi aussi tu es en avance, les espaces métriques j'avais pas vu ça en deuxieme année, du moins pas en cours.

[sandrine_guillerme]

Ok Monsieur le postier :lol3:

moi je suis à la bourre, parce que je sais que l'analyse c'est pas vraiment ma tasse de thé,
En avance par rapport à qui ? à ma fac ? on en avait fais chez moi .. mais donc je crois que tout dépend de là où tu taffes quoi..

P.S :Montpellier j'aime biéne (l'accent du sud que j'aime aussi) :lol4:

[legeniedesalpages]

Justement la topo c'est bien pour l'analyse, la continuité et les limites sont étudiées de façon très générale. On comprend beaucoup mieux ces notions après.

et l'accent du sud on le trouve plus dans les villages, dans la ville même, on l'a pas vraiment :ptdr:

[sandrine_guillerme]

Justement la topo c'est bien pour l'analyse, la continuité et les limites sont étudiées de façon très générale. On comprend beaucoup mieux ces notions après.

J'ai jamais dis le contraire !
Mais j'ai toujours eu plus du mal en analyse qu'en algèbre ou géométrie ..

et l'accent du sud on le trouve plus dans les villages, dans la ville même, on l'a pas vraiment :ptdr:

Hum, je suis déjà partie à Montpellier, C'est typique, mais bon plus on va loiéne (loin) plus on compran (comprend) moén (moins) :ptdr: :ptdr: (zkiffff )

Bon .. sur ce . j'y go, time to sleep (not for me .. ) mais j fatigue .. Sorry..

A demain, même heure même endroit . :party:

[sandrine_guillerme]

Bonjour,

Je remonte ce fil car j'ai finalement décidé de commencer la révision un peu .

Question bête pour commencer :

Si je veux calculer la signifiant la distance usuelle et les nombres irrationnels.

Je pense qu'on doit commencer par:

.

mais après ..

merci de m'aider là

[barbu23]

Sandrine, bonsoir :
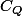
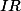
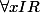
Tu peux commencer par remarquer Que est dense dans , donc , qui est un fermé n'est ce pas ?! donc il existe une suite tel que: .
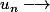
Alors, je te laisse conclure !!

[barbu23]

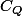
est inlus dans biensûr !!