Idéal maximal !!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Juin 2007, 11:00
par barbu23 » 26 Juin 2007, 11:00
Bonjour:
Soit
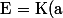 $)
une extension du corps

.
Soit
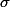
:
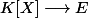
 $)
tel que:
 = a $)
et
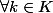
:
=k $)
.
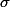
est l'unique homomorphisme d'anneau vérifiant ces conditions là.
Considerons le noyau de
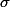
:
 = Ker(\sigma) $)
.
 $)
est un idéal principal ( c'est clair pourquoi).
Ma question : Pourquoi
 $)
est maximal.
et merçi infiniment !!!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Juin 2007, 11:06
par barbu23 » 26 Juin 2007, 11:06
J'ai une autre question à vous poser, hors sujet de départ :
Est ce que vous savez comment determiner le nombre de solutions d'une équation de la forme :
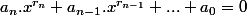
avec :
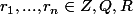
ou

mais pas dans

parceque c'est très connu !!!
et merçi infiniment !!!
j'espère qu'elle n'est pas stupide cette question , mais c'est juste par curiosité que je demande ça et merçi dans tous cas !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Juin 2007, 11:09
par tize » 26 Juin 2007, 11:09
Bonjour,
I(a) est un idéal principal car pour tout homomorphisme d'anneau Ker est un idéal, de plus K est un corps donc K[X] est principal donc I(a) est un idéal principal.
I(a) est maximal car (Théorème d'isomorphisme)
\sim E)
qui est un corps
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Juin 2007, 11:14
par yos » 26 Juin 2007, 11:14
Pour Z c'est facile : tu multiplies par
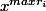
.
Pour Q tu poses
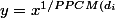})
où les
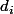
sont les dénominateurs des
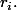
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Juin 2007, 11:43
par barbu23 » 26 Juin 2007, 11:43
Merçi beaucoup yos et tize !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Juin 2007, 19:16
par barbu23 » 26 Juin 2007, 19:16
Bonsoir:
j'ai une autre question à vous poser toujours sur le même sujet:
Posons :
 = \{ P(a) / P \in K[X] \} $)
.
Ma question est :
Pourquoi si

est algébrique alors
 = K[a] \approx K[X]/I(a) $)
?
Pourriez vous me dire ce que désigne ce symbole :
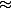
.. Est ce que c'est le signe d'isomorphisme .. comme
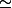
et merçi infiniment !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Juin 2007, 19:59
par tize » 26 Juin 2007, 19:59
Bonsoir,
oui je pense que c'est le symbole d'isomorphisme par contre que signifie pour toi K(X) par rapport à K[X] ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Juin 2007, 20:01
par barbu23 » 26 Juin 2007, 20:01
désolé:
 = \{ P \in K / P(a) = 0 \} $)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Juin 2007, 20:03
par yos » 26 Juin 2007, 20:03
A la main, ça donne :
Si a est algébrique, il existe P irréductible tel que P(a)=0.
Si
\neq 0)
, alors Q est non multiple de P, donc Q est premier avec P donc UP+VQ=1, donc en évaluant en a, V(a)Q(a)=1, donc Q(a) est inversible dans K[a], donc K[a] est un corps, donc K[a]=K(a)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Juin 2007, 20:05
par barbu23 » 26 Juin 2007, 20:05
Bonsoir tize:
D'après le cours:
 $)
est le plus petit sous corps engendré par
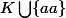
et
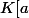
est le plus petit sous anneau engendré par
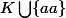
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Juin 2007, 20:09
par tize » 26 Juin 2007, 20:09
yos a écrit:A la main, ça donne :
Si a est algébrique, il existe P irréductible tel que P(a)=0.
Si
\neq 0)
, alors Q est non multiple de P, donc Q est premier avec P donc UP+VQ=1, donc en évaluant en a, V(a)Q(a)=1, donc Q(a) est inversible dans K[a], donc K[a] est un corps, donc K[a]=K(a)
Merci Yos c'est limpide et ça clôt le sujet... :we:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Juin 2007, 20:24
par yos » 26 Juin 2007, 20:24
Merci de ton jugement. On doit pouvoir faire plus pro, mais pour comprendre, c'est aussi bien comme ça.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
, alors Q est non multiple de P, donc Q est premier avec P donc UP+VQ=1, donc en évaluant en a, V(a)Q(a)=1, donc Q(a) est inversible dans K[a], donc K[a] est un corps, donc K[a]=K(a)