Flodelarab a écrit:Définitivement, non!
Si ton écriture est "quelque soit k entier" tu es en train de dire que l'exponentielle de tout nombre entier est égal à e ....
absurde.
vindiou, tu n'as pas lu la phrase du dessus !!! et cela change completement le sens de ma phrase :
Cesar a écrit:je precise que je n'ai pas ecrit: 
contrairement à ce que tu dis
alors que tu semble avoir que compris que je disais l'inverse .... :briques:
ce coup ci j'ai mis du gras et du souligné...histoire que tu le vois bien...
mais revenons au probleme : d'apres moi le principe de l'erreur vient du fait que l'on a changé - sans le dire - la valeur de k. on part avec k=1 et on passe alégrement à k = 0.
voici comment je vois le truc "propre" :
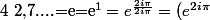^{\frac{1}{2i\pi}}=1^{\frac{1}{2i\pi}}=1)
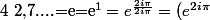^{\frac{1}{2i\pi})
à ce niveau, se situe un premier manque de rigueur on a

si on dit

on a fixé k = 1, sans le dire...pour éviter cela, il me semble honnete de faire :
^{\frac{1}{2i\pi}}= (e^{\frac{2ik\pi}{k}})^{\frac{1}{2i\pi}} = (e^{2ik\pi})^{\frac{1}{2ik\pi}} = 1^{\frac{1}{2ik\pi}})
à ce point là, on a pas fixé k, meme de maniere implicite...
ensuite vient le passage aux puissances de 1: à ce niveau, se situe le deuxieme manque de rigueur, car on fixe implicitement k = 0, ici aussi sans le dire. lorsqu'on ecrit :

alors que

on a fixé dans ce cas à la valeur k=0 sans le dire...
ici se pose un probleme : cette partie n'est pas bijective, écrire

est plutot limite, car il y a une infinité de reponses à mettre apres le "=".
mais si l'on écrit
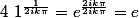
on retombe sur nos pieds, car k n'a pas varié..
que ceux qui sont encore éveillés reveillent ceux qui se sont endormis... :dodo:
