[1ere S] Petit exercice sur les suites...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par systemoframmfilth » 08 Mar 2007, 10:33
par systemoframmfilth » 08 Mar 2007, 10:33
Bonjour a tous!
Je m'entraine en faisant quelques exercices afin d'etre pret au contrôle ^^ mais il y en a un sur lequel je bute :S
Le voici :

Si quelqu'un pouvait m'aider ca serait vraiment génial, merci beaucoup d'avance!!
@+++++
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 08 Mar 2007, 11:11
par fonfon » 08 Mar 2007, 11:11
salut,
rappel:
Si
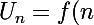)
ou f est une fonction de variable reelle monotone sur R+, la suite
)
a le même sens de variation que f
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 08 Mar 2007, 11:27
par Flodelarab » 08 Mar 2007, 11:27
systemoframmfilth a écrit:Si quelqu'un pouvait m'aider ca serait vraiment génial, merci beaucoup d'avance!!
Travaille le français plutôt ...
Pour les maths, ya fonfon :ptdr:
 par systemoframmfilth » 08 Mar 2007, 12:29
par systemoframmfilth » 08 Mar 2007, 12:29
je suis en S, le francais c'est pas mon trip, j'ai eu 12 et 13 au bac blanc donc ca va xD.
Sinon merci fonfon je vais reflechir a ta réponse.
 par systemoframmfilth » 08 Mar 2007, 18:08
par systemoframmfilth » 08 Mar 2007, 18:08
Je pense a trouver le signe de (Un+1 - Un) c'est une bonne idée ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 08 Mar 2007, 18:18
par fonfon » 08 Mar 2007, 18:18
tu te compliques etudies la fonction
=\frac{n^2+1}{2n^2})
(derivée..)
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 08 Mar 2007, 18:41
par Clembou » 08 Mar 2007, 18:41
Flodelarab a écrit:Travaille le français plutôt ...
Pour les maths, ya fonfon :ptdr:
Flodelarab, ton humour est imperissable je vois... mais c'est pas comme ça qu'on avancera dans la correction :triste:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 08 Mar 2007, 19:35
par Flodelarab » 08 Mar 2007, 19:35
Clembou a écrit:Flodelarab, ton humour est imperissable je vois... mais c'est pas comme ça qu'on avancera dans la correction :triste:
Dans la correction du francais ? ... ben ... j'aurais pu ecrire en gras en plus mais là, je pense qu'il a compris ce qu'il fallait dire.
De plus, si Fonfon m'avait pas griller au poteau j'aurais répondu la même chose avant lui :langue:
 par systemoframmfilth » 09 Mar 2007, 13:38
par systemoframmfilth » 09 Mar 2007, 13:38
Ok,(Un)=

où f : ]0:+infini[ -->N*
x --> (x²+1)/(2x²)
f = u/v avec u : x --> x²+1 dérivable sur ]0;+infini[ et v : x --> 2x² dérivable et ne s'annulant pas sur ]0;+infini[.
Pour tout x superieur à 0 u'(x) = 2x +0 =2x
Pour tout x superieur à 0 v'(x) = 2*2x = 4x
C'est bon pour le moment ? Pour savoir si je peux continuer.
Merci d'avance

-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Mar 2007, 14:08
par Flodelarab » 09 Mar 2007, 14:08
Et pkoi ne pas dire :
=\frac{x^2+1}{2x^2}=\frac{1}{2}+\frac{1}{2x^2}=\frac{1}{2}(1+\frac{1}{x^2}))
?
Or, on connait bien les variations de 1/x² donc ...
 par systemoframmfilth » 09 Mar 2007, 14:22
par systemoframmfilth » 09 Mar 2007, 14:22
Ah oui merci c'est bien plus simple comme ca ^^

x --> 1/x² décroissant sur ]0:+infini[
x --> 1 + (1/x²) décroissant sur ]0;+infini[ car 1 est positif
x --> 1/2 (1 + 1/x²) décroissant sur ]0;+infini[ car 1/2 est positif
Ainsi la suite (Un) est décroissante sur N*
C'est bon ?
Merci d'avance

-
couicsilver
- Membre Naturel
- Messages: 39
- Enregistré le: 03 Jan 2007, 21:47
-
 par couicsilver » 09 Mar 2007, 14:28
par couicsilver » 09 Mar 2007, 14:28
Juste une question, comment on trouve que u(n) <= 1 ? Par comparaison je trouve u(n) >= 1.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Mar 2007, 14:42
par Flodelarab » 09 Mar 2007, 14:42
systemoframmfilth a écrit:x --> 1 + (1/x²) décroissant sur ]0;+infini[ car 1 est positif
Mauvaise justification: -1 + (1/x²) est
aussi décroissant
Couicsilver, c'est donc que ta comparaison est fausse

Cela dit, je ne comprends pas ce que tu compares ... une simple récurrence suffit ...
 par systemoframmfilth » 09 Mar 2007, 14:45
par systemoframmfilth » 09 Mar 2007, 14:45
Comment pourrais-je jusifier? Juste en disant que quel que soit le nombre ajouté, la fonction de change pas de sens de variation ?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Mar 2007, 14:55
par Flodelarab » 09 Mar 2007, 14:55
systemoframmfilth a écrit:Comment pourrais-je jusifier? Juste en disant que quel que soit le nombre ajouté, la fonction de change pas de sens de variation ?
Oui.
OU sinon, tu peux dire que la composition de la fonction z->z+1 donne une fonction de meme sens de variation car z->z+1 est une fonction croissante.
Ou encore, tu peux revenir a la définition de la croissance....
a toi de voir
 par systemoframmfilth » 09 Mar 2007, 15:16
par systemoframmfilth » 09 Mar 2007, 15:16
Ok merci flo ;)
Par contre je ne sais comment procéder pour la 2eme question, pourrait-on m'aider ??
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Mar 2007, 15:49
par Flodelarab » 09 Mar 2007, 15:49
Flodelarab a écrit:une simple récurrence suffit ...
simple non ?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Mar 2007, 18:03
par Flodelarab » 09 Mar 2007, 18:03
systemoframmfilth a écrit:Je dois trouver U0 U1 U2 etc ??
3 étapes dans une récurrence:
- Rang 1: prouver que la ppté est vraie
- Rang n: on suppose la propriété vraie
- Rang n+1: prouver que la propriété est vraie.
Et c fini
 par systemoframmfilth » 09 Mar 2007, 18:50
par systemoframmfilth » 09 Mar 2007, 18:50
Mon cours parle juste de la definition par récurrence de la suite... :S
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités


 où f : ]0:+infini[ -->N*
où f : ]0:+infini[ -->N*