Intégrale convergente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
SuperPoule
- Membre Naturel
- Messages: 50
- Enregistré le: 03 Juin 2021, 09:09
-
 par SuperPoule » 20 Oct 2025, 20:16
par SuperPoule » 20 Oct 2025, 20:16
Bonjour,
Soit

de classe

sur
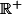
, strictement décroissante et qui tend vers

en

.
On pose
= \int_0^x f(t)dt -xf(x))
.
Comment montrer que si

est majorée alors
 dt)
converge ?

-
SuperPoule
- Membre Naturel
- Messages: 50
- Enregistré le: 03 Juin 2021, 09:09
-
 par SuperPoule » 20 Oct 2025, 22:05
par SuperPoule » 20 Oct 2025, 22:05
Je réponds à ma propre question :
On montre facilement que

est croissante. Si on suppose en plus que

est majorée alors
 = L\in\R^+)
.
Pour

, on a alors :
-F(x) = \int_x^y f(t) dt - yf(y)+xf(x) \geq \int_x^y f(y) dt- yf(y)+xf(x))
, car

est décroissante.
Donc :
-F(x) \geq (y-xf)(y)- yf(y)+xf(x) = xf(x)-xf(y))
.
Dans l'inégalité ainsi obtenue :
-F(x) \geq xf(x)-xf(y))
, en faisant tendre

et en se rappelant que
\underset{y\to+\infty}{\longrightarrow}0)
, on obtient :
 \geq xf(x) \geq 0)
reste à faire tendre
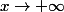
pour conclure que
\to0)
et on en déduit facilement que l'intégrale converge.
Du coup, je me demande maintenant s'il n'y a pas une façon de faire qui soit plus épurée ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités