Intégrale convergente

par **MacManus** » 31 Mar 2010, 17:56

Bonjour

Pour montrer que l'intégrale

est convergente, je peux par exemple faire le changement de variable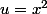

. Comment le démonter d'une manière générale ? merci pour vos précisions

par **Ben314** » 31 Mar 2010, 18:02

Je comprend pas trop, qu'entend tu par "d'une manière générale" ?

par **Ericovitchi** » 31 Mar 2010, 18:04

c'est vrai que l'on tombe sur

qui est un intégrale connue (

) il y a plusieurs façons de démontrer ça. Peut-être sur le forum.

par **MacManus** » 31 Mar 2010, 18:06

oui en fait il s'agit d'une intégrale impropre, et je voulais savoir comment procéder pour savoir si une telle intégrale converge ou pas (par équivalents - IPP - majoration...) en fait j'ai un peu oublier la façon de faire en qq sorte.

...

par **Joker62** » 31 Mar 2010, 18:06

Haileau.

Avec ton changement de variable, on s'en remet à calculer l'intégrale de 0 à l'infini de sin(u)/u
En 0 y'a pas de soucis.

Pour la convergence en l'infini, on fait une IPP il me semble ou bien on utilise le bourreau d'Abel.

Pour la calculer, on a le choix, les résidus, Laplace, intégrale à paramètre etc...

Edit : Bon on voulait juste la convergence, et grilled de partout :D

par **MacManus** » 31 Mar 2010, 18:07

ok c'est ce que j'avais fais aussi Ericovitchi. merci de confirmer

par **MacManus** » 31 Mar 2010, 18:10

ok merci Joker : ) (en fait je vais utiliser les résidus ds l'exo)

par **Ben314** » 31 Mar 2010, 18:13

Juste une remarque : pour des intégrales de ce type (convergentes mais non absolument convergentes), the "grosse méthode" c'est abel (sinon, il y a les "astuces" style I.P.P) mais surtout pas les équivalents (en tout cas pas directement...)

par **Ericovitchi** » 31 Mar 2010, 18:18

J'ai une méthode que j'aime bien c'est de dire que le 1/x vaut

et donc
I=

les puristes me diront si j'ai vraiment le droit de faire ça ;+)

par **Ben314** » 31 Mar 2010, 18:27

Je suis pas complètement sûr du fait que tu utilise Fubini sur des intégrales non absolument convergentes : donc c'est pas la "version basique" de Fubini.
Aprés, en gratant un peu, il y a peut-être une "version non basique" qui s'appliquerait ici (où alors on intègre de 0 à M sin(x)/x mais sa rend la méthode un peu moins jolie...)

par **Joker62** » 31 Mar 2010, 18:46

Le Fubini est à justifier très soigneusement parce que tel quel on peut pas l'appliquer !
Je l'ai fait en fermant les yeux lors d'un oral, et maintenant dès qu'on parle de Fubini, j'ai tout les yeux braqués sur moi lol :D

Intégrale convergente

intégrale convergente

Qui est en ligne