Calcul d'une intégrale
28 messages
- Page 2 sur 2 - 1, 2
Re: Calcul d'une intégrale
Bonjour à tous,
Il y a eu beaucoup de messages :
je pense que Stenam a la réponse à sa question dans le message de Pisigma (il me semble qu'un élève qui aborde des exercices de ce niveau doit reconnaître les dérivées de argsh et argch et arcsin,
ce qui épargne de devoir faire un changement de variable)
Pour la demande de Pisigma : on intègre de 0 à 1 une fonction continue sur [ 0 , 1 ]
Les propriétés de l'intégrale d 'une fonction continue permettent de dire que :
-)l'intégrale de 0 à 1 est la somme de l'intégrale de 0 à 1/2 et de l'intégrale de 1/2 à 1
(relation de Chasles)
-)pour 0<x<1/2 , l'intégrale de 0 à 1/2 est la limite , lorsque x tend vers 0 , de la fonction S définie par
S(x) = intégrale de x à 1/2 , et même principe au voisinage de 1
-) tout ceci pour travailler tranquillement dans ] 0 , 1[ afin d'y chercher une primitive F de la fonction à intégrer, on peut ainsi exprimer S(x) (au passage, pas besoin de calculer F(1/2) : cela va s'éliminer au final )
Est ce que ceci répond à vos questions ?
Cordialement
Il y a eu beaucoup de messages :
je pense que Stenam a la réponse à sa question dans le message de Pisigma (il me semble qu'un élève qui aborde des exercices de ce niveau doit reconnaître les dérivées de argsh et argch et arcsin,
ce qui épargne de devoir faire un changement de variable)
Pour la demande de Pisigma : on intègre de 0 à 1 une fonction continue sur [ 0 , 1 ]
Les propriétés de l'intégrale d 'une fonction continue permettent de dire que :
-)l'intégrale de 0 à 1 est la somme de l'intégrale de 0 à 1/2 et de l'intégrale de 1/2 à 1
(relation de Chasles)
-)pour 0<x<1/2 , l'intégrale de 0 à 1/2 est la limite , lorsque x tend vers 0 , de la fonction S définie par
S(x) = intégrale de x à 1/2 , et même principe au voisinage de 1
-) tout ceci pour travailler tranquillement dans ] 0 , 1[ afin d'y chercher une primitive F de la fonction à intégrer, on peut ainsi exprimer S(x) (au passage, pas besoin de calculer F(1/2) : cela va s'éliminer au final )
Est ce que ceci répond à vos questions ?
Cordialement
Re: Calcul d'une intégrale
On peut aussi remarquer que :
 = 2
= 2 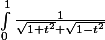
et s'affranchir ainsi des soucis liés à la borne 0
D'ailleur avec l'IPP que @Pisigma a explicité, il n'y a aucun problème et on trouve le résultat : pi/4 + 1/2 ln (1+sqrt2) - sqrt(2)/2
et s'affranchir ainsi des soucis liés à la borne 0
D'ailleur avec l'IPP que @Pisigma a explicité, il n'y a aucun problème et on trouve le résultat : pi/4 + 1/2 ln (1+sqrt2) - sqrt(2)/2
Re: Calcul d'une intégrale
intégrer de -1 à 1 n'améliore rien :
on a toujours t au dénominateur, donc un problème en 0.
Le résultat est bon
on a toujours t au dénominateur, donc un problème en 0.
Le résultat est bon
Re: Calcul d'une intégrale
c'est vrai ...
Dans la méthode que tu proposes, tu trouves une primitive dépendant de x ? lorsque tu fais tendres x vers 0 tu n'as aucun infini qui apparait ?
Dans la méthode que tu proposes, tu trouves une primitive dépendant de x ? lorsque tu fais tendres x vers 0 tu n'as aucun infini qui apparait ?
Re: Calcul d'une intégrale
Il n'y a pas d'infini : revoir mes messages précédents : la limite en 0 fait 0 (développement limité, pas trop compliqué)
A l'attention de Pisigma reprise de ma première réponse (qui commence à être un peu "noyée") :
Pour la demande de Pisigma : on intègre de 0 à 1 une fonction continue sur [ 0 , 1 ]
Les propriétés de l'intégrale d 'une fonction continue permettent de dire que :
-)l'intégrale de 0 à 1 est la somme de l'intégrale de 0 à 1/2 et de l'intégrale de 1/2 à 1
(relation de Chasles)
-)pour 0<x<1/2 , l'intégrale de 0 à 1/2 est la limite , lorsque x tend vers 0 , de la fonction S définie par
S(x) = intégrale de x à 1/2 , et même principe au voisinage de 1
-) tout ceci pour travailler tranquillement dans ] 0 , 1[ afin d'y chercher une primitive F de la fonction à intégrer, on peut ainsi exprimer S(x) (au passage, pas besoin de calculer F(1/2) : cela va s'éliminer au final )
Est ce que ceci répond à vos questions ?
A l'attention de Pisigma reprise de ma première réponse (qui commence à être un peu "noyée") :
Pour la demande de Pisigma : on intègre de 0 à 1 une fonction continue sur [ 0 , 1 ]
Les propriétés de l'intégrale d 'une fonction continue permettent de dire que :
-)l'intégrale de 0 à 1 est la somme de l'intégrale de 0 à 1/2 et de l'intégrale de 1/2 à 1
(relation de Chasles)
-)pour 0<x<1/2 , l'intégrale de 0 à 1/2 est la limite , lorsque x tend vers 0 , de la fonction S définie par
S(x) = intégrale de x à 1/2 , et même principe au voisinage de 1
-) tout ceci pour travailler tranquillement dans ] 0 , 1[ afin d'y chercher une primitive F de la fonction à intégrer, on peut ainsi exprimer S(x) (au passage, pas besoin de calculer F(1/2) : cela va s'éliminer au final )
Est ce que ceci répond à vos questions ?
28 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
