La fabrication d'une table nécessite 12 planches. La probabilité
qu'une planche présente un noeud dans le bois, ce qui fragilise
la table, est de 0,04.
On note X la variable aléatoire qui, à tout lot de 12 planches
prélevées au hasard et avec remise, associe le nombre de
planches fragiles dans le lot. Chacun de ces lots sert à fabriquer
une table.
Une table est mise en vente au tarif normal si elle possède au
plus une planche fragile. Elle n'est pas mise en vente si elle
possède plus de trois planches fragiles. Elle est vendue en pro-
motion dans les autres cas.
Montrer que la variable x suit une loi binomiale et donner ses paramètres.
Calculer P(X=0) et P ( X=1)
Déterminer P(X_<1)
Mathématiques
13 messages
- Page 1 sur 1
2 planches
Bonjour,
Qu'as-tu essayé ?
À part l'habillage, c'est une application assez immédiate de ton cours.
Quant à l'habillage, c'est vraiment un exemple parfait de truc complètement idiot. Le comble est l'histoire du tirage avec remise pour constituer un lot de 12 planches ! Si vous remettez dans le tas une planche dès que vous l'avez tirée, vous n'aurez jamais votre lot de 12 !

Ephsizov, tu n'es nullement responsable de cette idiotie ; c'est la personne qui a concocté cet énoncé.
Qu'as-tu essayé ?
À part l'habillage, c'est une application assez immédiate de ton cours.
Quant à l'habillage, c'est vraiment un exemple parfait de truc complètement idiot. Le comble est l'histoire du tirage avec remise pour constituer un lot de 12 planches ! Si vous remettez dans le tas une planche dès que vous l'avez tirée, vous n'aurez jamais votre lot de 12 !


Ephsizov, tu n'es nullement responsable de cette idiotie ; c'est la personne qui a concocté cet énoncé.
Re: Maths loi binomiale
Bonjour,
L’habillage est (malheureusement) assez classique tout de même. Ce qu’il faut comprendre selon moi c’est que sur un immense stock de N planches où on pense qu'il y en a 0.04N de fragiles et 0.96N de normales, on prélève uniquement 12 planches. Comme N est très grand devant 12, on a très peu de chances de choisir deux fois la même planche même en la remettant dans le stock à chaque fois. Autrement dit on peut faire comme s'il s’agissait d’un tirage avec remise (traduire mathématiquement par les conditions d’approximation d’une loi hypergéométrique par une loi binomiale sont vérifiées). Ceci dit je n’aurais sans doute pas écrit l’énoncé ainsi non plus.
L’habillage est (malheureusement) assez classique tout de même. Ce qu’il faut comprendre selon moi c’est que sur un immense stock de N planches où on pense qu'il y en a 0.04N de fragiles et 0.96N de normales, on prélève uniquement 12 planches. Comme N est très grand devant 12, on a très peu de chances de choisir deux fois la même planche même en la remettant dans le stock à chaque fois. Autrement dit on peut faire comme s'il s’agissait d’un tirage avec remise (traduire mathématiquement par les conditions d’approximation d’une loi hypergéométrique par une loi binomiale sont vérifiées). Ceci dit je n’aurais sans doute pas écrit l’énoncé ainsi non plus.
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
Re: Maths loi binomiale
Ce qui m'horripile, c'est cette obsession de faire "concret" qui pousse à inventer du pseudo-concret de pacotille. Au final, tout l'effort dépensé pour cacher le problème mathématique derrière cette histoire de planches n'aboutit qu'à faire des nœuds ... dans la tête de l'élève.
Re: Maths loi binomiale
Je parie qu'après ça, l'énoncé donne le prix de vente d'une table "normale", le rabais fait sur table fragile mais tout de même mise en vente, et demande l'espérance de la somme obtenue pour une table.
On voit bien le réalisme de la situation : le fabricant prend 12 planches sans les contrôler, il fabrique la table et une fois qu'elle est fabriquée il la met au rebut quand il s'aperçoit que plus de trois des planches ont des noeuds !
On voit bien le réalisme de la situation : le fabricant prend 12 planches sans les contrôler, il fabrique la table et une fois qu'elle est fabriquée il la met au rebut quand il s'aperçoit que plus de trois des planches ont des noeuds !

Re: Maths loi binomiale
Les maths, ça sert à quoi ? à résoudre des problèmes de la vie courante.
Traduire un problème de la vie courante en équations, c'est un vrai besoin. Et c'est une vraie difficulté pour beaucoup d'étudiants.
Donc, c'est très bien que des exercices s'appuient sur des situations réelles.
Mais effectivement, l'expression 'avec remise' dans ce contexte est complètement ridicule.
Traduire un problème de la vie courante en équations, c'est un vrai besoin. Et c'est une vraie difficulté pour beaucoup d'étudiants.
Donc, c'est très bien que des exercices s'appuient sur des situations réelles.
Mais effectivement, l'expression 'avec remise' dans ce contexte est complètement ridicule.
Re: Maths loi binomiale
lyceen95 a écrit:Donc, c'est très bien que des exercices s'appuient sur des situations réelles.
Franchement, que trouves-tu de "réel" dans la situation de l'énoncé ?
Les maths, ça sert à quoi ? à résoudre des problèmes de la vie courante.
C'est une vision un peu réductrice des maths.
Re: Maths loi binomiale
J'ai mieux comme prolongement, on peut calculer la probabilité que le fabricant fasse faillite et se retrouve banni de tous les forums de maths pour ne pas avoir écouté les matheux lambda qui lui auraient suggéré de vérifier les planches avant de fabriquer la table.
Blague à part, cela fait partie intégrante de mon métier de donner du sens à des énoncés de prof pour préparer les étudiants à l'examen donc j'en ai vu passé des centaines d'exercices sur les probas avec habillage et celui là n'est quand même pas terrible.
C'est pas le pire car au moins il n'y a pas d’ambiguïté sur la réponse mais pour bien faire, l'énoncé aurait du laisser entendre qu'on répète des épreuves identiques et indépendantes avec chaque épreuve qui comporte 2 issues : fragile ou normale.
Par exemple, une chaine de fabrication découpe des planches de manière conforme ou non et fabrique la table automatiquement dès qu'il y a 12 planches de découpées, c'est pas génial mais c'est déjà mieux.
On peut argumenter que l'on sait d’expérience depuis toujours que la probabilité d'être découpée non conformément pour une planche est de 0.04 en toutes circonstances.
Je suis désolée mais là le contexte est un peu bancal, la probabilité donnée correspond forcément à la fréquence nombre de planches fragiles / nombre de planches total dans le stock initialement. Sauf que dès qu'on prend une planche, la probabilité sur les planches restantes change obligatoirement puisque à minima le dénominateur change.
Ils ont collé une rustine en disant qu'il y a remise de la planche mais ça se voit que c'est une rustine. Bref, le prof qui a écrit l'énoncé n'était visiblement pas inspiré, ça arrive aux meilleurs, mais force est de constater que le résultat n'est pas très pédagogique et ne correspond pas vraiment au réel non plus.
Blague à part, cela fait partie intégrante de mon métier de donner du sens à des énoncés de prof pour préparer les étudiants à l'examen donc j'en ai vu passé des centaines d'exercices sur les probas avec habillage et celui là n'est quand même pas terrible.
C'est pas le pire car au moins il n'y a pas d’ambiguïté sur la réponse mais pour bien faire, l'énoncé aurait du laisser entendre qu'on répète des épreuves identiques et indépendantes avec chaque épreuve qui comporte 2 issues : fragile ou normale.
Par exemple, une chaine de fabrication découpe des planches de manière conforme ou non et fabrique la table automatiquement dès qu'il y a 12 planches de découpées, c'est pas génial mais c'est déjà mieux.
On peut argumenter que l'on sait d’expérience depuis toujours que la probabilité d'être découpée non conformément pour une planche est de 0.04 en toutes circonstances.
Je suis désolée mais là le contexte est un peu bancal, la probabilité donnée correspond forcément à la fréquence nombre de planches fragiles / nombre de planches total dans le stock initialement. Sauf que dès qu'on prend une planche, la probabilité sur les planches restantes change obligatoirement puisque à minima le dénominateur change.
Ils ont collé une rustine en disant qu'il y a remise de la planche mais ça se voit que c'est une rustine. Bref, le prof qui a écrit l'énoncé n'était visiblement pas inspiré, ça arrive aux meilleurs, mais force est de constater que le résultat n'est pas très pédagogique et ne correspond pas vraiment au réel non plus.
Modifié en dernier par Kekia le 31 Mar 2022, 21:16, modifié 1 fois.
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
Re: Maths loi binomiale
J'ai peut-être mal formulé mon point de vue.
De manière générale, je trouve que c'est très bien qu'un exercice de maths soit formulé comme un cas concret. (2 trains partent de A et B bla bla ).
Mais évidemment, celui-ci est complètement raté.
Les maths, ça sert à résoudre des problèmes de la vie courante. Oui, c'est réducteur, mais c'est aussi 'optimiste'.
Pour 70% de la population, les maths, ça ne sert à rien, pour 29.5% de la population, ça sert à résoudre les problèmes de la vie courante , et pour les 0,5% restants, ça sert à beaucoup plus que ça. J'ai choisi une position moyenne, pas vraiment moyenne !
De manière générale, je trouve que c'est très bien qu'un exercice de maths soit formulé comme un cas concret. (2 trains partent de A et B bla bla ).
Mais évidemment, celui-ci est complètement raté.
Les maths, ça sert à résoudre des problèmes de la vie courante. Oui, c'est réducteur, mais c'est aussi 'optimiste'.
Pour 70% de la population, les maths, ça ne sert à rien, pour 29.5% de la population, ça sert à résoudre les problèmes de la vie courante , et pour les 0,5% restants, ça sert à beaucoup plus que ça. J'ai choisi une position moyenne, pas vraiment moyenne !
Re: Maths loi binomiale
Et à quel pourcentage de la population estimes-tu les gens qui, dans leur vie courante, utilisent des technologies qui doivent tout ou énormément aux maths - même si les maths utilisées n'ont pas été développées dans ce but ?
Je sais très bien que le travail de modélisation est très important et souvent très difficile. Mais justement, le genre d'habillage pseudo-concret dont l'exercice dont on cause est un exemple caricatural est à l'opposé d'un travail sérieux de modélisation.
Je sais très bien que le travail de modélisation est très important et souvent très difficile. Mais justement, le genre d'habillage pseudo-concret dont l'exercice dont on cause est un exemple caricatural est à l'opposé d'un travail sérieux de modélisation.
Re: Maths loi binomiale
Tout le monde se sert de protocole cryptographique pour les paiements par carte bancaire. C'est fondamentalement basé sur les maths et d'ailleurs la plupart d'entre nous font confiance sans même connaitre les différents algorithmes de chiffrements.
Je pense qu'avoir des notions de probas/stats fait partie des notions utiles dans la vie courante, je rêverai que tout le monde comprenne ce qu'est un degré de signification, ce qu'on peut conclure ou non à partir d'une étude pour éviter certaines dérives antiscientifiques.
Si on écrit calculer) et
et ) pour
pour  qui suit une loi binomiale
qui suit une loi binomiale 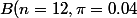) (ou alors
(ou alors 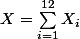 avec
avec  iid selon une loi de Bernoulli de paramètre
iid selon une loi de Bernoulli de paramètre 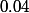 ) l'exercice se vide un peu de son sens je trouve d'autant que n'importe quel logiciel peut le faire.
) l'exercice se vide un peu de son sens je trouve d'autant que n'importe quel logiciel peut le faire.
Parler de travail sérieux de modélisation pour des exercices scolaires me parait trop optimiste car on ne peut pas vérifier si les choix faits sont confortés ou non par les observations or c'est indispensable en réalité.
Une phase de traduction du langage courant vers le langage mathématiques me parait un bon compromis et ce n'est pas inutile pour la compréhension des notions par les étudiants mais le curseur est sans doute difficile à placer correctement dans l’enseignement. Dans cet exercice, c'est loupé, mais je suis d'accord avec lyceen95 sur le fait qu'il est bien d'essayer de le faire.
Pour info, j'ai cherché un peu dans les annales et à priori cet exercice est pour des BTS CGO (Comptabilité et Gestion des Organisations) http://sterling-maths-doumer.over-blog.com/article-bts-blanc-n-1-sujet-41312897.html
Je pense qu'avoir des notions de probas/stats fait partie des notions utiles dans la vie courante, je rêverai que tout le monde comprenne ce qu'est un degré de signification, ce qu'on peut conclure ou non à partir d'une étude pour éviter certaines dérives antiscientifiques.
Si on écrit calculer
Parler de travail sérieux de modélisation pour des exercices scolaires me parait trop optimiste car on ne peut pas vérifier si les choix faits sont confortés ou non par les observations or c'est indispensable en réalité.
Une phase de traduction du langage courant vers le langage mathématiques me parait un bon compromis et ce n'est pas inutile pour la compréhension des notions par les étudiants mais le curseur est sans doute difficile à placer correctement dans l’enseignement. Dans cet exercice, c'est loupé, mais je suis d'accord avec lyceen95 sur le fait qu'il est bien d'essayer de le faire.
Pour info, j'ai cherché un peu dans les annales et à priori cet exercice est pour des BTS CGO (Comptabilité et Gestion des Organisations) http://sterling-maths-doumer.over-blog.com/article-bts-blanc-n-1-sujet-41312897.html
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
 Mathématiques
Mathématiques
Exercice 1
Une entreprise fabrique des tables de jardin en bois. La fabrication d'une table nécessite 12
planches. La probabilité qu'une planche présente un nœud dans le bois, ce qui la fragilise, est 0,04.
On note X la variable aléatoire donnant le nombre de planches fragiles par table à la sortie de la
fabrication.
1. Montrer que la variable aléatoire X suit une loi binomiale et donner ses paramètres.
2. Calculer P(X = 0) et P(X = 1).
3. Déterminer P(X < 1).
Une table est mise en vente au prix normal si elle possède au maximum une planche fragile. Elle
n'est pas mise en vente si elle possède plus de 3 planches fragiles. Elle est vendue en promotion
dans les autres cas.
4. Déduire des résultats précédents la probabilité qu'une table soit vendue au prix normal.
5. Par un raisonnement similaire, calculer :
a. La probabilité que la table ne soit pas vendue.
b. La probabilité que la table soit vendue en promotion.
6. Calculer le nombre moyen de planches fragiles par table.
Une entreprise fabrique des tables de jardin en bois. La fabrication d'une table nécessite 12
planches. La probabilité qu'une planche présente un nœud dans le bois, ce qui la fragilise, est 0,04.
On note X la variable aléatoire donnant le nombre de planches fragiles par table à la sortie de la
fabrication.
1. Montrer que la variable aléatoire X suit une loi binomiale et donner ses paramètres.
2. Calculer P(X = 0) et P(X = 1).
3. Déterminer P(X < 1).
Une table est mise en vente au prix normal si elle possède au maximum une planche fragile. Elle
n'est pas mise en vente si elle possède plus de 3 planches fragiles. Elle est vendue en promotion
dans les autres cas.
4. Déduire des résultats précédents la probabilité qu'une table soit vendue au prix normal.
5. Par un raisonnement similaire, calculer :
a. La probabilité que la table ne soit pas vendue.
b. La probabilité que la table soit vendue en promotion.
6. Calculer le nombre moyen de planches fragiles par table.
Re: Mathématiques
Bonjour Ephsizov,
Le principe est que ce soit toi qui fasse l'exercice avec de l'aide si besoin, peux tu nous dire ce que tu as commencé et où tu bloques ?
On a un petit peu débattu de l’intérêt de l'exercice mais on est à ta disposition désormais et il y a consensus sur le fait que suit une loi binomiale de paramètre
suit une loi binomiale de paramètre 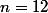 et
et 
Le principe est que ce soit toi qui fasse l'exercice avec de l'aide si besoin, peux tu nous dire ce que tu as commencé et où tu bloques ?
On a un petit peu débattu de l’intérêt de l'exercice mais on est à ta disposition désormais et il y a consensus sur le fait que
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
