Réciproque

[jonjuste3364]

Bonsoir, je bloque à un exercice sur la réciproque. J'arrives à faire l'initialisation mais je bloque à l'hérédité.
Les données sont :
Un+1=3Un/1+Un
0<Un<1
Merci d'avance

[mathelot]

Bonsoir,
il s'agit de démonstration par récurrence.
Que vaut le 1er terme ?
On définit la fonction f par:
avec
les deux points fixes de f sont 0 et 2.

[jonjuste3364]

u0 vaut 1/2.
Comment je dois faire du coup?

[mathelot]

On pose les inégalités de récurrence:


- Estc e que l'assertion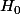 est vraie ?
- Quel est le sens de variation de la fonction f, avec ?
on pose
comment en déduire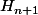 en utilisant la fonction f ?

[jonjuste3364]

Pourquoi <2 et pas à 1 ?

[mathelot]

Pourquoi <2 et pas à 1 ?

parce que 0 et 2 sont les deux points fixes de f: f(0)=0 et f(2)=2

on encadre entre ces deux points fixes


qu'as tu trouvé pour le sens de variation de f ?

[jonjuste3364]

J'ai trouvé que f était positive jusqu'à -1/2 puis negative jusqu'à 1/3 puis positive jusqu'à + infini

[mathelot]

on étudie le signe de la fonction dérivée f':

que vaut f'(x) ?

[jonjuste3364]

f'(x) = 3/2

[mathelot]

on pose et
et

[mathelot]

pour le sens de variation de f sur l'intervalle [0;2]:
f est strictement .... sur [0;2]

[mathelot]

Soit l'hypothèse

f étant strictement croissante sur [0;2], elle conserve la relation d'ordre:




L'hypothèse est donc héréditaire.