Une rationalisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 24 Oct 2021, 07:10
par Dacu » 24 Oct 2021, 07:10
Bonjour à tous ,
Rationaliser le dénominateur de la fraction
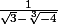
.
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 24 Oct 2021, 08:26
par lyceen95 » 24 Oct 2021, 08:26
Rappel : a²-b²=(a-b)(a+b)
Ca ne suffit pas, mais tu connais probablement d'autres identités remarquables du même type.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 24 Oct 2021, 13:21
par tournesol » 24 Oct 2021, 13:21
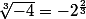
Rationaliser
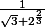
-
mathelot
 par mathelot » 24 Oct 2021, 18:04
par mathelot » 24 Oct 2021, 18:04
Bonsoir,
utiliser l'identité
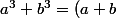(a^2-ab+b^2))
le dénominateur devient:
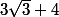
puis l'identité
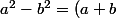(a-b))
le dénominateur devient:
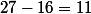
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 25 Oct 2021, 05:58
par Dacu » 25 Oct 2021, 05:58
mathelot a écrit:Bonsoir,
utiliser l'identité
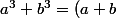(a^2-ab+b^2))
le dénominateur devient:
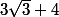
puis l'identité
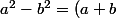(a-b))
le dénominateur devient:
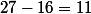
Bonjour,
Quelles sont les racines du troisième ordre du nombre
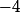
et quelles sont les racines du deuxième ordre du nombre

?Quelles sont les valeurs de

et

dans le cas de votre raisonnement ?Merci beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 25 Oct 2021, 08:08
par lyceen95 » 25 Oct 2021, 08:08
Tu n'as pas besoin de connaître les racines du 3ème ordre ... ou du 2ème ordre ...
Mais si tu y tiens, la racine du 3ème ordre de -4, c'est
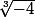
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 25 Oct 2021, 10:18
par tournesol » 25 Oct 2021, 10:18
Le symbole
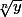
ne désigne pas l'ensemble des racines n_iemes de y mais:
si n est pair : l'unique antécédent positif du réel y positif par la fonction x->

.
Si n est impair : l'unique antécédent du réel y par la fonction x->

.
Si n est impair , x->

est impaire et donc
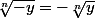
Ici n=3 et
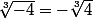
Tu dois donc rationaliser
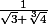
comme te l'a expliqué mathelot .
-
mathelot
 par mathelot » 25 Oct 2021, 10:35
par mathelot » 25 Oct 2021, 10:35
re,
=(3-3^{1/2}4^{1/3}+4^{2/3})/(3 \times 3^{1/2}+4))
=(3-3^{1/2}4^{1/3}+4^{2/3})(3 \times 3^{1/2} -4)/11)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités