Volume de sphère et derive

par **leog** » 27 Oct 2006, 17:47

je dérive le volume d'une sphère et j'obtiens sa surface; je dérive sa surface et j'obtiens quatre fois la valeur du périmètre.. pourkoi?

par **tbotw69** » 27 Oct 2006, 17:57

Euh, à volume constant ?? Précise l'enoncé !

par **Quidam** » 27 Oct 2006, 23:21

leog a écrit:je dérive le volume d'une sphère et j'obtiens sa surface; je dérive sa surface et j'obtiens quatre fois la valeur du périmètre.. pourkoi?

Et pourquoi pas ?

Tu penses avoir trouvé une règle : encore faudrait-il la préciser !

Moi je dérive le volume d'une sphère, j'obtiens sa surface. Pourquoi ? Parce que la variation de volume de la sphère quand le rayon augmente est égale au volume de la partie de la nouvelle sphère située à l'extérieur de l'ancienne sphère, qui se trouve, en première approximation pour un petit accroissement du rayon, être égal au produit de la surface de sa base (la surface de la sphère) par "son épaisseur", la variation du rayon.

Moi je dérive la surface d'un disque, j'obtiens son périmètre. Pourquoi ? Parce que la variation de surface du disque quand le rayon augmente est égale à la surface de la partie du nouveau disque située à l'extérieur de l'ancien disque, qui se trouve, en première approximation pour un petit accroissement du rayon, être égal au produit de la longueur de sa base (le périmètre du disque) par "sa hauteur", la variation du rayon.

Dans les deux cas, la dérivée est la "grandeur" en dimension n-1 de la limite de l'objet de dimension n : pour l'espace de dimension 3, la "grandeur" en question est l'aire de la surface (dimension 2) qui limite la sphère, pour l'espace de dimension 2, la "grandeur" en question est la longueur de la ligne (dimension 1) qui limite le disque.

Par contre le périmètre de la sphère, ne mesure pas la limite qui définit la sphère.

Ma foi, je n'ai pas d'autre explication à te proposer ! Et je dis : pourquoi pas ?

par **scelerat** » 28 Oct 2006, 15:09

leog a écrit:je dérive le volume d'une sphère et j'obtiens sa surface; je dérive sa surface et j'obtiens quatre fois la valeur du périmètre.. pourkoi?

C'est quoi le perimetre d'une surface sans bord ?

par **Gato** » 19 Nov 2006, 22:59

Le volume d'une sphère c'est 0 non ?

par **alben** » 20 Nov 2006, 13:21

Bonjour
Une sphère de dimension 1, contient un segment de droite
Une sphère de dimension 2, contient un disque
Une sphère de dimension 3, contient une boule ordinaire
Une sphère de dimension 4, contient une boule de dim 4
etc
Meme chose pour les pavés qui sont respectivement segment, carrés, cubes, hypercubes...
Maintenant, calculons les volumes de pavés et de boules de diamètre =1.
dim1 pavé=1, boule=1
dim2 pavé=1, boule=

dim3 pavé=1, boule=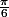

dim4 pavé=1, boule=

etc...
Combien peut-on ecraser d'hyper-pommes de dimension 6 dans une hyperboite de même dimension pour préparer une hyper compote ?

Quelle est la limite pour dim->infini ?
Conclure sur l'intérêt économique des fabricants de compote à rester en dimension 3

par **ddy** » 14 Déc 2006, 13:52

parce que 4 est le rapport (incroyablement simple) des surfaces de 2 objets très differents:

surface de la sphere = 4 pi R²
surface du disque = pi R²

par **Zebulon** » 14 Déc 2006, 19:20

Bonsoir,

alben a écrit:Combien peut-on ecraser d'hyper-pommes de dimension 6 dans une hyperboite de même dimension pour préparer une hyper compote ?

Conclure sur l'intérêt économique des fabricants de compote à rester en dimension 3

:happy3: :we: :ptdr: :lol:

Volume de sphère et derive

volume de sphère et derive

Qui est en ligne