Sphère et cylindre

[chan79]

Salut à tous
Un peu de calcul, pour ne pas perdre la main pendant les vacances.
[img][IMG]http://img526.imageshack.us/img526/4905/sph.png[/img][/IMG]
On creuse une sphère en bois de rayon R pour y insérer un cylindre dont l'axe passe par le centre de la sphère. Le rayon du cylindre est r.
Calculer le rapport r/R pour qu'exactement la moitié du volume de bois de la sphère soit enlevée.
Niveau lycée

[Zweig]

Je trouve

[chan79]

Je trouve

Salut
tu as dû oublier deux calottes sphériques

[Zweig]

Le volume occupé par le cylindre dans la sphère est bien ?

[Zweig]

Le volume occupé par le cylindre dans la sphère est bien ?

[Kikoo <3 Bieber]

Je trouve idem

Développement :

Prenons une coupe normale à l'axe du cylindre. On constate que l'aire de la couronne externe vaut pi(R²(x)-r²(x)).
On veut sommer de -R à R la valeur de cette couronne pour les x réels, afin de déterminer le volume de la boule creusée.
Or r(x) est constant...
Plaçons-nous dans un repère (O;i,j). Avec les coordonnées cartésiennes, il est clair que y = R(x) = \sqrt{R²-x²}, d'où :
A = \pi S{-R -> R} (R²-x²-r²)dx = \pi [R²x - (x^3)/3 - r²x]{-R -> R} = \pi [(4R^3)/3 -2Rr²]

Or on veut que A = (1/2)V_B = (4\pi R^3)/6
Ce qui équivaut à chercher r tel que :
\pi R((4R²)/3 -2r²)=4\pi R^3/6
Après un peu de calculs, on trouve r = (1/(\sqrt{3}))R
D'où le rapport.

Edit : même erreur...

Je reprends :
On doit multiplier par deux au niveau de l'intégrale, car sinon, nous ne sommons que d'un seul côté, et pas de l'autre.
Finalement, le rapport est de (\sqrt{2})/2

[Kikoo <3 Bieber]

Re : non, je dois tout reprendre ^^...

[Dlzlogic]

Bonjour,
Moi, je ferais comme Beagle, je creuserais d'abord un petit trou, et je pèserais soigneusement les copeaux de bois et la sciure. J'agrandirais le trou, jusqu'à obtenir un poids de sciure exactement égal à la moitié du poids de la boule. Bien-sûr, il ne faut pas oublier de peser la boule avant toute intervention, de noter son poids et de savoir faire une division par 2.

[chan79]

Bonjour,
Moi, je ferais comme Beagle, je creuserais d'abord un petit trou.

On peut aussi se creuser un peu la tête :ptdr:

[Kikoo <3 Bieber]

Bonjour,
Moi, je ferais comme Beagle, je creuserais d'abord un petit trou, et je pèserais soigneusement les copeaux de bois et la sciure. J'agrandirais le trou, jusqu'à obtenir un poids de sciure exactement égal à la moitié du poids de la boule. Bien-sûr, il ne faut pas oublier de peser la boule avant toute intervention, de noter son poids et de savoir faire une division par 2.

Ouais, mais avec les imprécisions :p

On peut aussi se creuser un peu la tête :ptdr:

Pas facile quand ya déjà pas grand chose... :wrong:

[Dlzlogic]

Pour l'instant, je suis entrain de compter tous les chemins possibles pour aller d'un point à un autre, la menuiserie, ce sera pour ce week-end.

[Zweig]

Je sais que le volume d'un segment sphérique (volume délimité par deux sections parallèles de rayons r et r' séparées d'une hauteur h) est donnée par

Mais ça, c'est dans le cas où les sections sont verticales, ici on a des sections horizontales, donc apparemment la formule n'est plus valable ...

[Kikoo <3 Bieber]

intéressant! :ptdr:

quelqu'un sait comment exprimer le volume des deux trous par r ou R?

Euh, tu veux parler du volume du cylindre ? :p

[Kikoo <3 Bieber]

Pour l'instant, je suis entrain de compter tous les chemins possibles pour aller d'un point à un autre

Une infinité... ^^ Non ?

[Dlzlogic]

Une infinité... ^^ Non ?

Non, c'est pas si simple que ça, on doit passer par des points (noeuds) en nombre fini.
La liaison directe (arc) entre deux points, si elle existe est unique.
On ne peut emprunter un arc qu'une seule fois.
Mais depuis que l'ai appris que le maximum de capacité cérébrale est obtenu vers ?? ans, ça fait un bout de temps que la mienne décroit.

[Luc]

Je pense qu'ici le problème se ramène à un problème plan au vu de la symétrie de révolution autour de l'axe du cylindre. => on se ramène à un rectangle de largeur 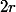centré dans un cercle de rayon .
J'arrive à exprimer la surface occupée par le rectangle comme une fonction de , et je me ramène à résoudre l'équation , où et .

Du coup il n'y a pas de solution exacte, mais une solution approchée valant à peu près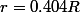 . Je n'en suis que moyennement convaincu en fait, même si la valeur numérique semble plausible.

Luc

Je sais que le volume d'un segment sphérique (volume délimité par deux sections parallèles de rayons r et r' séparées d'une hauteur h) est donnée par

Mais ça, c'est dans le cas où les sections sont verticales, ici on a des sections horizontales, donc apparemment la formule n'est plus valable ...

[Dlzlogic]

Par manque de temps, je n'ai pas cherché, mais ça me rappelle vraiment le problème de la chèvre qui doit de limiter à brouter la moitié de son champ rond et elle doit calculer la longueur de sa corde attachée à un piquet de clôture.

[C.Ret]

Du coup il n'y a pas de solution exacte, mais une solution approchée valant à peu près . Je n'en suis que moyennement convaincu en fait, même si la valeur numérique semble plausible.

Mon programme de CAO me donne une valeur très proche: r/R = 0.40397
Avec une sphère de 5cm, il annonce un volume retiré (cylindre à l'intérieur de la sphère et les deux calottes) d'environ 261.8 cm3.

Mais, ne me demandez pas comment il fait son calcul. J'imagine par une méthode itérative basée sur un nombre important d'éléments finis.

[Mathusalem]

Moi je trouve

Détail :

On pose z^2 = 1 - (r/R)^2
Alors, le volume des deux calottes est
V_2cal = 2pi/3 R^3 ( 2 - 3z + z^3 )
Le volume du cylindre de rayon r entre les deux calottes vaut
V_cyl = 2pi r^2 R z

Et on veut V_2cal + V_cyl = 2pi/3 R^3
d'où r/R = sqrt(1-1/2^(2/3))