Bonjour, je suis en première et pour nous entraîner sur un futur contrôle, notre professeur de Mathématique nous à donner plusieurs exercices !
Voici le premier surement tout bête mais que j'ai du mal à cerner
Soit (Un) définie pour tout entier naturel n par Un = 4n + 1 - 1/2(puissance)n
Calculer la somme U0 + U1 + ... + U20
Calculer une suite, j'ai appris, mais ce n'était pas si poussé ! Quelqu'un pourrait m'éclaircir ?
Somme d'une suite
7 messages
- Page 1 sur 1
Re: Somme d'une suite
Il y a trois morceaux dans  : d'abord
: d'abord  , puis
, puis  , enfin
, enfin  .
.
Pour chacun de ces trois morceaux, tu peux essayer de calculer la somme pour allant de 0 à 20.
allant de 0 à 20.
Peut-être verras-tu alors, pour chacun de ces morceaux, à quelle type de suite tu as affaire ?
Pour chacun de ces trois morceaux, tu peux essayer de calculer la somme pour
Peut-être verras-tu alors, pour chacun de ces morceaux, à quelle type de suite tu as affaire ?
Re: Somme d'une suite
Merci ! Je pense avoir compris. pour avoir la somme de U0+U1+...+U20, je calcule les 3 séparément et les additionne par la suite ?
Re: Somme d'une suite
Oui, c'est l'idée. Mais fais attention quand tu parles d'additionner, il y a tout de même un signe - quelque part.
Re: Somme d'une suite
GaBuZoMeu a écrit:Oui, c'est l'idée. Mais fais attention quand tu parles d'additionner, il y a tout de même un signe - quelque part.
Re, alors je rencontre un problème durant l'exerice !
Pour calculer une somme des n premiers termes d'une suite géométrique on utilise l'expression U0 *( 1-qn+1 /1-q)
Sauf que dans le cas de 1/2n, bah U0 = 0 ... à moins que U0=1 ??
Re: Somme d'une suite
Salut !
Par convention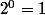

Par convention
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Somme d'une suite
Je suis bien d'accord que  , mais je ne dirais pas que c'est une convention. C'est une conséquence de la définition.
, mais je ne dirais pas que c'est une convention. C'est une conséquence de la définition.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
