Conplexes : racine nième
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Nov 2006, 19:20
par sue » 24 Nov 2006, 19:20
salut!
je cherche à démontrer que
)

et en déduire que :
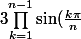= \frac{n}{2^{n-1}})
un indice pour la 1ère svp ?
merci :we:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Nov 2006, 20:15
par Imod » 24 Nov 2006, 20:15
Essaie de résoudre dans

l'équation
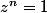
.
Imod
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Nov 2006, 20:17
par sue » 24 Nov 2006, 20:17
bon j'ai trouvé les racines de l'équation
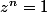
:

t.q

ça m'aide ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Nov 2006, 20:19
par sue » 24 Nov 2006, 20:19
oui Imod merci , c'est ce que je viens de faire comment puis-je exploiter ça ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Nov 2006, 20:23
par sue » 24 Nov 2006, 20:23
en fait je dois démontrer mnt que :
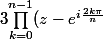 = 0)
??
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Nov 2006, 20:24
par Imod » 24 Nov 2006, 20:24
Je ne suis pas très au courant des programmes de terminal et peut-être ma piste n'est pas la bonne mais si
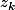
est une solution de

alors

peut se mettre en facteur dans
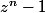
.
Imod
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 24 Nov 2006, 20:26
par Elsa_toup » 24 Nov 2006, 20:26
Non, pas la peine.
Tu sais que les racines de l'équation
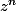
= 1 vérifient donc l'équation
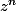
-1 = 0 (c'est la même équation...).
Donc que tu peux écrire
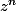
-1 comme le produit de (z - racine).
C'est ce qu'on te demande !
(Tu te souviens que si a est racine du polynome P(x), alors on peut écrire : P(x) = (x-a)*Q(x) ?)
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Nov 2006, 20:43
par sue » 24 Nov 2006, 20:43
oui uoi merci c'était trop bete :briques:
sinon pour la 2ème voilà ce que j'ai fait :
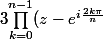 = e^{i\frac{2\pi}{n}} \prod_{k=0}^{n-1} (1-e^{i\frac{2(k-1)\pi}{n}}) =e^{i\frac{2\pi}{n}} \prod_{k=0}^{n-1} -2i sin(\frac{\pi(k-1)}{n}) = 2^{n-1}e^{i\frac{2\pi}{n}} \prod_{k=0}^{n-1}- i sin(\frac{\pi(k-1)}{n}) = ...)
suis-je sur la bonne voie ? (je réfléchis à la suite )
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Nov 2006, 21:11
par sue » 24 Nov 2006, 21:11
je crois que je suis bloqué là :triste:
pourriez-vous m'aiguillé ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Nov 2006, 21:52
par sue » 24 Nov 2006, 21:52
je crois que je suis bloqué là :triste:
pourriez-vous m'aiguillé ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités