Dérivé nieme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 14:16
par abcd22 » 15 Jan 2006, 14:16
Les dérivées sont justes mais pas les valeurs en 0
}(0)=0,\ f^{(4)}(0)=1, f(0)=0)
.
Oui c'est Mac-Laurin epsilon.
-
Anonyme
 par Anonyme » 15 Jan 2006, 14:23
par Anonyme » 15 Jan 2006, 14:23
Et f^(2) (0)= 1 alors car f^(2) (x) = f^(4) (x)
Donc f(x) = 0+0+x²/2!+ x^3/3! + x^4/4! + x^5/5! f^(5) (c)
La c'est bon ?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 14:25
par abcd22 » 15 Jan 2006, 14:25
Non f''(0)=0, c'est périodique seulement à partir de n=3 à cause du x² dans l'expression de f !
-
Anonyme
 par Anonyme » 15 Jan 2006, 14:27
par Anonyme » 15 Jan 2006, 14:27
Ben je comprend pas les dérivées sont les deux memes et y'a plus de x² !!
A moin que je me sois trompé dans les derivées ?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 14:29
par abcd22 » 15 Jan 2006, 14:29
Les dérivées sont justes, et il y a un -1 en plus dans f'' (qui vient de la dérivée seconde de -x²/2).
-
Anonyme
 par Anonyme » 15 Jan 2006, 14:39
par Anonyme » 15 Jan 2006, 14:39
Ok c'est pour ca que je comprenais pas alors
Je reprend donc :
f(0)=0
f'(x) = (e^x - e^-x)/2 - x
f'(0) = 0
f''(x)= (e^x + e^-x)/2 - 1
f''(0)=0
f'''(x)=(e^x - e^-x)/2
f'''(0)=0
f^(4) (x) = (e^x+e^-x)/2
f^'4) (0) = 1
f^(5) (x) = (e^x - e^-x)/2
Donc f(x) = 0+0+0+0+ x^4/4! + x^5/5! f^(5) (c)
f(x) = x^4/4! + x^5/5! f^(5) (c)
Voila , je pense que tout doit etre correct comme cela ?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 14:43
par abcd22 » 15 Jan 2006, 14:43
Oui c'est correct ! N'hésite pas à demander pour la suite !
-
Anonyme
 par Anonyme » 15 Jan 2006, 14:46
par Anonyme » 15 Jan 2006, 14:46
Ben la 4. me bloque deja , car je pense que y'a un developpement a faire pour en deduire que f(x)>= 0 ?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 14:54
par abcd22 » 15 Jan 2006, 14:54
x^4 est positif sur R, donc ce qui pose problème, c'est le
}(c))
.
Il faut montrer que c'est positif, donc étudier le signe de f^(5), en écrivant
}(x) = e^x\left(\frac{1-e^{-2x}}{2}\right))
par exemple...
-
Anonyme
 par Anonyme » 15 Jan 2006, 15:01
par Anonyme » 15 Jan 2006, 15:01
Ben pour x <0 ca tend vers - linfini , pour x proche de 0 ca tend vers 0 et pour x>0 ca tend vers linfini , non ?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 15:05
par abcd22 » 15 Jan 2006, 15:05
Oui mais ça ne suffit pas de dire les limites, il pourrait y avoir des variations bizarres entre deux avec plein de changements de signe... Avec l'écriture que j'ai donnée on peut dire facilement le signe de f^(5) pour x>0 et x<0.
-
Anonyme
 par Anonyme » 15 Jan 2006, 15:11
par Anonyme » 15 Jan 2006, 15:11
Oui ca tend toujours vers 0 comme on multiplie la division par e^x...
Je vois pas trop la le rapprochement avec la question de depart.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 15:21
par abcd22 » 15 Jan 2006, 15:21
On voudrait déduire de
 = \frac{x^4}{4!} + \frac{x^5}{5!} f^{(5)}(c))
que f est positive, donc comme x^4 est positif, on voudrait bien montrer que
}(c))
est positif aussi.
Si
}(c) \geq 0 \ \mathrm{pour}\ c > 0)
.
-
Anonyme
 par Anonyme » 15 Jan 2006, 15:30
par Anonyme » 15 Jan 2006, 15:30
Ok mais c'est la démonstration le plus compliqué..
-
Anonyme
 par Anonyme » 15 Jan 2006, 16:15
par Anonyme » 15 Jan 2006, 16:15
Je n'arrive pas a démontrer !!! snif
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 16:22
par abcd22 » 15 Jan 2006, 16:22
On cherche le signe de
}(x) = e^x \left( \frac{1-e^{-2x}}{2} \right) = e^{-x} \left( \frac{e^{2x}-1}{2} \right))
, ça doit mieux se voir sur la dernière écriture en fait :
- quel est le signe de

sur R ?
- et celui de

sur
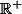
? et sur
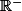
?
-
Anonyme
 par Anonyme » 15 Jan 2006, 16:32
par Anonyme » 15 Jan 2006, 16:32
Pourquoi cela ?
On a dit que f^(5) (x) = (e^x - e^-x)/2
je comprends plus :(
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 16:36
par abcd22 » 15 Jan 2006, 16:36
On factorise par
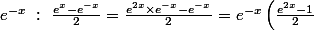)
.
-
Anonyme
 par Anonyme » 15 Jan 2006, 16:40
par Anonyme » 15 Jan 2006, 16:40
OK donc le signe est toujours positif...
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 15 Jan 2006, 16:45
par abcd22 » 15 Jan 2006, 16:45
Le signe de
})
ou celui de
})
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
