Continuité à droite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 25 Aoû 2019, 16:31
par lyceen95 » 25 Aoû 2019, 16:31
mehdi-128 a écrit:@Lycéen
Un extrait de mon livre. Ça change tout le temps de définition, c'est incompréhensible :
La fonction

est continue à droite en

si
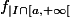
Puis :
La limite à droite de

en

est la limite de
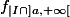
en

lorsque cette dernière est définie.
Où est le problème ? On parle de continuité à droite dans la 1ère définition, et de limite à droite dans la 2ème.
Ce sont 2 concepts proches, mais différents, et donc c'est normal d'avoir 2 définitions différentes.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Aoû 2019, 17:03
par mehdi-128 » 25 Aoû 2019, 17:03
Ok lycéen.
Par contre comment utiliser directement la définition de mon livre pour montrer que
)
n'est pas continue à gauche en
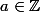
?
Soit
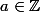
Il faut montrer que
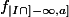
n'est pas continue. Posons
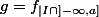
D'après le cours :

continue au voisinage de

implique

continue en a.
Or
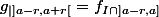
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 25 Aoû 2019, 17:26
par Tuvasbien » 25 Aoû 2019, 17:26
Vraiment je ne comprends pas pourquoi tu te perds avec autant de formalisme alors que la réponse est sous tes yeux, à la vue du graphe on comprend immédiatement que la partie entière n'est pas continue en tous les entiers puisque là où par exemple
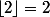
on a

pour tout
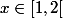
qui est un voisinage à gauche de

donc

donc
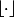
n'est pas continue à gauche en 2 !
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Aoû 2019, 18:03
par mehdi-128 » 25 Aoû 2019, 18:03
Tuvasbien a écrit:Vraiment je ne comprends pas pourquoi tu te perds avec autant de formalisme alors que la réponse est sous tes yeux, à la vue du graphe on comprend immédiatement que la partie entière n'est pas continue en tous les entiers puisque là où par exemple
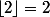
on a

pour tout
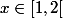
qui est un voisinage à gauche de

donc

donc
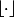
n'est pas continue à gauche en 2 !
Mais je ne comprends pas d'après mon cours ils parlent de la restriction
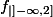
donc un voisinage à gauche de 2 est
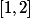
ou
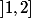
.
Pourquoi vous ouvrez l'intervalle en 2 ? J'ai même cherché sur internet, un voisinage à gauche de

c'est
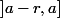
donc bien fermé en

.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Aoû 2019, 18:13
par mehdi-128 » 25 Aoû 2019, 18:13
Vous utilisez peut être la notion de voisinage épointé mais elle n'a pas encore été abordée à ce stade du livre donc comment faire sans cette notion en prenant simplement l'intervalle ]1,2] par exemple ?
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 25 Aoû 2019, 18:40
par Tuvasbien » 25 Aoû 2019, 18:40
La définition de

est la limite en
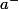
de

est :
-\ell|<\varepsilon)
La définition de

est continue en

à gauche est :
-f(a)|<\varepsilon)
ce qui est équivalent à
-f(a)|<\varepsilon)
(ce n'est pas le cas pour la limite, il est possible que
-\ell|\geqslant\varepsilon)
pour un certain

). On peut encore le réécrire
=f(a))
.
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 25 Aoû 2019, 18:41
par Tuvasbien » 25 Aoû 2019, 18:41
Si on prenait dans la définition de la limite l'intervalle
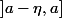
alors dans ce cas l'égalité
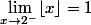
serait fausse, la limite n'existerait même pas !
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Aoû 2019, 18:57
par mehdi-128 » 25 Aoû 2019, 18:57
Ok pour les définitions. A ce stade de l'exemple les limites à gauche et à droite ne sont pas encore définies. Elles le sont 2 pages à la suite.
Si on note
=\lfloor x\rfloor)
comment montrer que
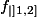
n'est pas continue en

? Ça montrerait d'après le cours que

n'est pas continue en

.
Quand on se place au voisinage à gauche de

qui est
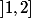
pourquoi
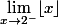
n'existe pas ?
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 25 Aoû 2019, 19:01
par Tuvasbien » 25 Aoû 2019, 19:01
Elle existe (je dis juste que si on remplaçait l’intervalle ouvert par un intervalle fermé dans la définition ça marcherait pas c’est pourquoi on prend un intervalle ouvert), sur [1,2[, f est constante et sa valeur est différente de f(2) donc la limite en 2^- de f est différente de f(2) donc f est pas continue à gauche en 2
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Aoû 2019, 19:22
par mehdi-128 » 25 Aoû 2019, 19:22
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 25 Aoû 2019, 19:30
par Tuvasbien » 25 Aoû 2019, 19:30
Il va falloir qu’on m’explique comment on définit la notion de continuité sans avoir defini la notion de limite, d’autant plus que ton livre n’est pas la bible, si on te pose cette question à un oral on attendra une réponse simple, c’est quoi tes « r » dans tes propositions ? D’ailleurs comment on montre qu’une fonction est pas continue en un point ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Aoû 2019, 20:37
par mehdi-128 » 25 Aoû 2019, 20:37
Tuvasbien a écrit:Il va falloir qu’on m’explique comment on définit la notion de continuité sans avoir defini la notion de limite, d’autant plus que ton livre n’est pas la bible, si on te pose cette question à un oral on attendra une réponse simple, c’est quoi tes « r » dans tes propositions ? D’ailleurs comment on montre qu’une fonction est pas continue en un point ?
La notion de limite a été définie mais pas celle de limite à gauche et à droite. Donc ici il faut travailler avec la restriction
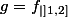
est montrer que

n'est pas continue.
Pour montrer qu'une fonction n'est pas continue en 1 point mon livre donne une méthode : il suffit d'exhiber une suite
)
convergeant vers

et telle que
))
ne converge pas vers
)
Je ne connais pas d'autre méthode...
Par exemple, ici posons
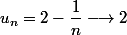
et
=1 \ne f(2))
Car
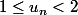
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 25 Aoû 2019, 20:51
par Tuvasbien » 25 Aoû 2019, 20:51
Les notions de limite, limite à gauche et limite à droite sont analogues comme les notions de continuité, continuité à gauche et continuité à droite, ce qui change c'est juste le voisinage sur lequel on se place. Concernant la suite, ça montre que

n'est pas continue en

mais aussi que

n'est pas continue en

à gauche puisque
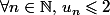
. C'est quand même idiot de la part du livre de proposer un exercice sur une notion pas encore définie... La définition avec la restriction est la même qu'avec les quantificateurs alors pourquoi les différenciées ? D'autant plus que la définition avec les quantificateurs est la plus utilisée de loin.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Aoû 2019, 21:03
par mehdi-128 » 25 Aoû 2019, 21:03
Oui par ailleurs j'ai du mal à manipuler les restrictions. J'y verrai peut être plus clair dans la suite en traitant des exercices concrets de limites à gauche et à droite.
Merci.
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 25 Aoû 2019, 21:05
par Tuvasbien » 25 Aoû 2019, 21:05
J'en suis sûr.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 25 Aoû 2019, 21:33
par mehdi-128 » 25 Aoû 2019, 21:33
J'ai fait le même travail pour la partie entière par excès.
Elle est continue à gauche sur

. Il suffit de prendre
+1)
et de considérer
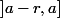
Elle est continue à droite sur
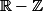
. Il suffit de prendre
-1)
et de considérer
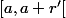
Elle n'est pas continue en
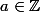
il suffit de considérer
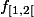
et la suite
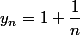
. On a
=2 \ne f(1)=1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
est continue à droite en
si
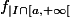
en
est la limite de
en
lorsque cette dernière est définie.
