Continuité à droite + égalité presque partout

[Gogogo99]

Bonjour,

J'ai un peu de mal à montrer que:

f et g continues à droite sur R
f=g presque partout sur R pour la mesure de Lebesgue

alors f=g

Quand l'hypothèse est continue (et pas seulement à droite ou à gauche) et quand on travaille sur des intervalles [a;b], j'arrive à le montrer avec un argument de topologie général et le fait qu'un ouvert de mesure de Lebesgue nulle est forcément vide.

[mrif]

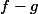
S'il existe tel que soit différent de alors il existe un intervalle sur lequel ne s'annule jamais puisque f et g sont continues à droite. Je te laisse conclure puisque .

[Gogogo99]

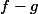
S'il existe tel que soit différent de alors il existe un intervalle sur lequel ne s'annule jamais puisque f et g sont continues à droite. Je te laisse conclure puisque .

L'ensemble des points de différences de f et g est discret au plus dénombrable.
Or la mesure de Lebesgue de ton intervalle vaut Epsilon >0.

[Gogogo99]

Oui alors c'est plutôt

[x0;x0+E[ sera inclus dans E={ points de différences de f et g}

Comme mesure(E)=0 on a mesure([x0;x0+E[)=0 , contradiction.

Merci

[mrif]

Oui c'est à peu près ça.

Je concluerais plutôt comme ça:
f et g sont distinctes sur un intervalle de mesure (de Lebesgue) non nulle donc l'hypothèse de départ est fausse.

Attention: l'ensemble des points de différences de f et g n'est pas nécessairement discret ni dénombrable.

[mrif]

Oui alors c'est plutôt

[x0;x0+E[ sera inclus dans E={ points de différences de f et g}

Comme mesure(E)=0 on a mesure([x0;x0+E[)=0 , contradiction.

Merci

Oui ça c'est bon.

Dans ma réponse précédente je n'avais pas connaissance de ton nouveau message.