aviateur a écrit:Mais t'es con ou quoi?
Sii.e
mais aussi
d'où la contradiction.
Où est-ce que c'est bidon?
Insulte + n'importe quoi. Tu devrais dormir, ça ira mieux demain.
aviateur a écrit:Mais t'es con ou quoi?
Sii.e
mais aussi
d'où la contradiction.
Où est-ce que c'est bidon?
aviateur, hier soir a écrit:Mais t'es con ou quoi?
Ce qui est bidon, c'est que tu dises qu'il faut calculer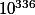
le même, ce matin a écrit:Bon on est d'accord pour terminer ma démo il reste à montrer que
Quand on fait ça, on applique bien un algorithme pour vérifier que 2016 est l'ordre multiplicatif de 10 modulo 2017 (algorithme qui consiste à factoriser 2016 et à vérifier ce qui se passe pour le quotient de 2016 par chacun de ses diviseurs premiers). Il y a confusion entre "faire les calculs à la main" et "ne pas utiliser un algorithme". L'algorithme d'Euclide est un algorithme, même quand on fait les calculs à la main.
aymanemaysae a écrit:est un nombre premier donc
.
Supposons qu'il existetel que
, alors on a
est un multiple de
, donc
est le plus petit entier qui vérifie
.
GaBuZoMeu a écrit:aymanemaysae, tu lis mal le théorème de Carmichael et tu lui fais dire n'importe quoi !
Attention au quantificateur : Carmichael dit que si POUR TOUT entier a premier à n, a^m = 1 modulo n, alors lambda(n) divise m. Il ne dit certainement pas que si, pour un certain a fixé premier à n (par exemple a=10), a^m = 1 modulo n, alors lambda(n) divise m.
Ça va, tu es bien d'accord que ton "argument" ne vaut pas ?
aymanemaysae a écrit:
Enfin , commedonc
est le plus petit nombre entier
non nul qui vérifie
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 97 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :